The farm is semicircular from a profile pipe. The main points of calculation of metal trusses

A farm is a simple architectural structure with a multi-purpose purpose. Most often, it is needed to protect a small recreation area from bright sunlight and unexpected precipitation, or as an alternative to a covered building on the site of a country cottage. Metal pipes are used as a material for the durability of the structure. But before starting construction work, you will need the correct calculation of the farm from the profile pipe for the canopy.

Advantages of profile pipes for trusses

Profile pipes have a number of advantages:

1. Optimal stability under significant external loads, due to which the canopy does not deform or collapse.
2. Affordable price finished product, because hollow metal pipes are used as the starting material.
3. Lightweight due to filling the internal cavity of the profile pipes with air.
4. Excellent durability.
5. Long service life.
6. The ability to implement the most complex design options without investing a lot of time and effort.
7. The admissibility of its manufacture by one's own hands with the correct calculation of the farm from metal pipe(read also: "").

The use of profile pipes of various shapes

To date, such tubular products are relevant in mechanical engineering. Agriculture, construction, furniture production. Due to the specific properties of profile pipes, it is possible to implement the most original projects for the creation of floors, spans, supporting structures, frames for the subsequent construction of facilities. The same modern billboards are made using profile pipes.

Canopies were no exception. In order for the design to be guaranteed to be reliable and budgetary, it is better to use a profiled pipe as a material (read: ""). The optimal solution is products with square and rectangular sections. If you adhere to the dimensions of the drawing, from which it is clear how to weld a truss from a profile pipe, you will get a stable structure.

The main nuances of the finished product

Any building structure is supported by a properly planned special system or truss. You can’t just change its geometric dimensions, even when changing rigid nodes to articulated ones. If the bars do not carry loads outside the node, then the truss components are compressed or stretched. Such systems can be created using straight rods connected by nodes of tubular trusses. That is, the result is an original hanging structure, including the upper and lower chords with uprights and braces between them.

Today, modern construction is unthinkable without the use of trusses. But most often the latter are in demand in the construction of coatings of huge spans. According to this principle, sports complexes, bridges, stages, podiums, pavilions, etc. are being built. Anyone who needs such a structure can buy it ready-made or weld it from pipes on their own, but first you need to figure out how to calculate a canopy from a profile pipe.

Consider last option, representing a long and laborious event.

It includes:

1. Determination of the exact amount of pipe material for the future farm and the degree of pressure on the elements of the system.
2. A responsible approach to the selection of material for a triangular truss. Lightweight profiled pipes with square section. This is where a good design comes in.
3. Making a drawing of a truss from a profiled pipe, taking into account the characteristics of each part. According to it, in the future, the entire building will be assembled.
4. The last stage is the implementation of installation work, on which the reliability and duration of the operational capabilities of the structure depend. And for a positive result, you need to know thoroughly how to properly weld trusses from a profile pipe. See also: "".

The choice of truss design from rectangular elements depends on:

• span length;
• placement of the attic floor;
• roof pitch angle.

How to calculate a farm

Here are the standard steps for this procedure:

1. Selection of the desired triangular truss scheme, oriented to the required configuration. At the same time, attention is paid to the main function of the canopy, materials for its construction, and other characteristics.
2. Determining the exact dimensions of the future design. For example, the height depends on the type of roof and the materials used. With a span of more than 36 meters, it will be necessary to additionally calculate one more parameter - the construction lift, which is related to the extinguished bend - the opposite of the pressure on the truss.
3. Calculation of the dimensions of building panels that clearly correspond to the distance between structural elements that transmit loads in the system. Next is the determination of the length between nodes. Most often, this parameter is considered identical to the width of the panel. See also: "".

According to a similar scheme, but with its own specific nuances, it is possible to calculate an arched truss from a profile pipe. As a guide, it is better to take the standard steps of the procedure.

After determining all the digital values ​​\u200b\u200bfor the construction of the future farm, you need to enter them into the formulas and enter them into the appropriate computer program, which will give a clear design scheme. And only after all these actions, you can start studying another, no less serious matter ─ how to properly weld a truss from a profile pipe. The quality of further installation work depends on the professionalism of specialists in this field.

There is an open area measuring 10x5 m near the house and I want to make this area closed so that in the summer you can drink tea on the street, regardless of the weather conditions, more precisely looking, but from under a reliable canopy, and also so that you can put the car under a canopy, saving on the garage, and indeed to be protected from the heat of the sun on a summer day. Here are just 10 meters - the span is large and it is difficult to pick up a beam for such a span, and this very beam will be too massive - it is boring and generally resembles a factory floor. In such cases best option- make trusses instead of beams, and then throw a crate on the trusses and make a roof. Of course, the shape of the truss can be any, but the calculation of the triangular truss will be considered below, as the simplest option. The problems of calculating columns for such a canopy are considered separately; the calculation of two trusses with parallel chords or crossbars, on which the trusses will rest, is also not given here.

For now, it is assumed that the trusses will be located in increments of 1 meter, and the load on the truss from the crate will be transferred only at the nodes of the truss. roofing material will serve as corrugated board. The height of the farm can theoretically be any, but only if it is a canopy adjacent to the main building, then the main limiter will be the shape of the roof, if the building is one-story, or windows on the second floor, if there are more floors, but in any case, it is unlikely to make the farm height more than 1 m it will work out, and taking into account the fact that you also need to do a crossbar between the columns, then 0.8 m will not always work out (nevertheless, we will accept this figure for calculations). Based on these assumptions, it is already possible to design a farm:

Figure 272.1. The general preliminary scheme of the canopy on farms.

Figure 272.1 shows the beams of the crate in blue, the truss to be calculated in blue, purple- beams or trusses on which columns rest, a color change from light blue to dark purple in this case indicates an increase in the design load, which means that darker structures will require more powerful profiles. The trusses in Figure 272.1 are shown in dark green due to the completely different nature of the load. Thus, the calculation of all structural elements separately, such as:

Sheathing beams (sheathing beams can be considered as multi-span beams, if the length of the beams is about 5 m, if the beams are made about 1 m long, i.e. between trusses, then these are ordinary single-span beams on hinged supports)

Roof trusses (it is enough to determine the normal stresses in the cross sections of the rods, which will be discussed below)

Beams or trusses under roof trusses (calculated as single-span beams or trusses)

presents no particular problems. However, the purpose of this article is to show an example of the calculation of a triangular truss, and this is what we will do. In Figure 272.1, 6 triangular trusses can be considered, while the load on the extreme (front and back) trusses will be 2 times less than on the rest of the trusses. This means that these two farms, if there is a strong desire to save on materials, should be calculated separately. However, for aesthetic and technological reasons, it is better to make all trusses the same, which means that it is enough to calculate all only one truss (shown in blue in Fig. 272.1). In this case, the farm will be console, i.e. the truss supports will not be located at the ends of the truss, but at the nodes shown in Figure 272.2. Such a design scheme allows you to more evenly distribute the load, and therefore use profiles of a smaller section for the manufacture of trusses. For the manufacture of trusses, it is planned to use square profile pipes of the same type, and further calculation will help to select the required section of the profile pipe.

If the beams of the crate will rest on top of the truss nodes, then the load from the canopy of corrugated board and snow lying on this corrugated board can be considered concentrated, applied at the truss nodes. The truss rods will be welded together, while the rods of the upper chord will most likely be continuous, approximately 5.06 m long. However, we will assume that all truss nodes are hinged. These clarifications may seem like an insignificant trifle, but they allow you to speed up and simplify the calculation as much as possible, for the reasons outlined in another article. The only thing left for us to determine for further calculations is the concentrated load, but this is not difficult to do if the corrugated board or batten beams have already been calculated. When calculating corrugated board, we found out that corrugated board sheets with a length of 5.1-5.3 m are a multi-span continuous beam with a cantilever. This means that the support reactions for such a beam and, accordingly, the loads for our truss will not be the same, however, the changes in the support reactions for the 5th span beam will not be so significant, and to simplify the calculations, we can assume that the load from snow, corrugated board and battens will be transferred uniformly, as in the case of single-span beams. Such an assumption will only lead to a small margin of safety. As a result, we get the following calculation scheme for our farm:

Figure 272.2. Design scheme for a triangular truss.

Figure 272.2 a) shows the general design scheme of our farm, the design load is Q = 190 kg, which follows from the calculated snow load of 180 kg / m 2, the weight of the corrugated board and possible weight sheathing beams. Figure 272.2 b) shows the sections, thanks to which it is possible to calculate the forces in all the truss rods, taking into account the fact that the truss and the load on the truss is symmetrical and it means that it is enough to calculate not all the truss rods, but a little more than half. And in order not to get confused in the numerous rods in the calculation, it is customary to mark the rods and truss nodes. The marking shown in Fig. 272.2 c) means that the farm has:

Rods of the lower belt: 1-a, 1-c, 1-d, 1-g, 1-i;

Rods of the upper belt: 2-a, 3-b, 4-d, 5-e, 6-h;

Braces: a-b, b-c, c-d, d-e, e-e, e-g, f-h, h-i.

If each truss rod is calculated, then it is advisable to draw up a table in which all the rods should be entered. Then it will be convenient to enter the obtained value of compressive or tensile stresses into this table.

Well, the calculation itself does not present any particular difficulties if the truss is welded from 1-2 types of closed section profiles. For example, the entire calculation of the truss can be reduced to calculating the forces in the bars 1st, 6th and 3rd. To do this, it is enough to consider the longitudinal forces that arise when cutting off a part of the farm along the line IX-IX (Fig. 272.2 d).

But let's leave the sweet for the third, and see how it's done on more simple examples, for this we consider

section I-I (Fig. 272.2.1 e)

If we cut off the excess part of the truss in the indicated way, then it is necessary to determine the forces in only two truss rods. For this, the equations of static equilibrium are used. Since there are hinges at the truss nodes, the value of the bending moments at the truss nodes is zero, and in addition, based on the same conditions of static equilibrium, the sum of all forces about the axis X or axes at is also equal to zero. This allows at least three equations of static equilibrium to be drawn up (two equations for forces and one for moments), but in principle there can be as many equations of moments as there are nodes in a truss, and even more if Ritter points are used. And these are the points at which two of the forces under consideration intersect and, with a complex geometry of the truss, the Ritter points do not always coincide with the nodes of the truss. Nevertheless, in this case, we have a fairly simple geometry (we will still have time to get to complex geometry), and therefore, the available truss nodes are sufficient to determine the forces in the rods. But at the same time, again, for reasons of simplicity of calculation, such points are usually chosen, the equation of moments with respect to which allows you to immediately determine the unknown force, without bringing the matter to the solution of a system of 3 equations.

It looks like this. If we draw up an equation of moments with respect to point 3 (Fig. 272.2.2 e), then it will have only two terms, and one of them is already known:

M 3 \u003d -Q l/2 + N 2-a h = 0;

N 2-a h \u003d Ql / 2;

where l - the distance from point 3 to the point of application of the force Q / 2, which in this case is the shoulder of the force, according to the design scheme adopted by us l = 1.5 m; h- arm of the force N 2-a(shoulder shown in Fig. 272.2.2 e) in blue).

In this case, the third possible term of the equation is zero, since the force N 1-a (in Fig. 272.2.2 e) is shown in gray) is directed along the axis passing through point 3 and hence the action arm is equal to zero. The only thing that we do not know in this equation is the shoulder of the force N 2-a, however, it is easy to determine it, having the appropriate knowledge of geometry.

Our farm has an estimated height of 0.8 m and a total estimated length of 10 m. Then the tangent of the angle α will be tgα = 0.8/5 = 0.16, respectively, the value of the angle α = arctgα = 9.09 o. And then

h = l sinα

Now nothing prevents us from determining the value of force N 2-a:

N 2-a = Q l/(2lsinα ) = 190/(2 0.158) = 601.32 kg

In the same way, the value N 1-a. To do this, an equation of moments is drawn up with respect to point 2:

M 2 \u003d -Q l/2 + N 1-a h = 0;

N 1-a h = Q l/2

N 1-a = Q/(2tgα ) = 190/(2 0.16) = 593.77 kg

We can check the correctness of the calculations by compiling the force equations:

ΣQ y \u003d Q / 2 - N 2-a sinα = 0; Q/2 = 95= 601.32 0.158 = 95 kg

ΣQ x = N 2-a cosα - N 1-a = 0; N 1-a = 593.77 = 601.32 0.987 = 593.77 kg

The static equilibrium conditions are met and any of the force equations used for verification could be used to determine the forces in the bars. That, in fact, is all, the further calculation of the farm is pure mechanics, but just in case, we will consider

section II-II (Fig. 272.2. e)

At first glance, it seems that the equation of moments about point 1 will be simpler to determine the force N a-b, however, in this case, to determine the shoulder of the force, you first need to find the value of the angle β. But if we consider the equilibrium of the system relative to point 3, then:

M 3 \u003d -Q l/2 - Q l/3 + N 3-b h = 0;

N 3-b h = 5Q l/6 ;

N 3-b = 5Q/(6sinα ) = 5 190/(6 0.158) = 1002.2 kg(works in tension)

Well, now let's determine the value of the angle β. Based on the fact that all aspects of a certain right triangle(the lower leg or the length of the triangle is 1 m, the side leg or the height of the triangle is 0.16 m, the hypotenuse is 1.012 m, and even the angle α), then the neighboring right triangle with a height of 0.16 m and a length of 0.5 m will have tgβ = 0.32 and, accordingly, the angle between length and hypotenuse β = 17.744 o, obtained from the arc tangent. And now it's easier to formulate the equation of forces about the axis X :

ΣQ x = N 3-b cosα + N a-b cosβ - N 1-a = 0;

N a-b = (N 1-a - N 3-b cosα )/cosβ = (593.77 - 1002.2 0.987)/ 0.952 = - 415.61 kg

In this case, the "-" sign shows that the force is directed in the opposite direction from that which we accepted when drawing up the design scheme. And then it's time to talk about the direction of forces, more precisely, about the meaning that is invested in this direction. When we replace internal forces in the considered cross section of the truss rods, then the force directed from the cross section means tensile stresses, if the force is directed towards the cross section, then compressive stresses are meant. From the point of view of static equilibrium, it does not matter which direction of the force to take in the calculations, if the force is directed in the opposite direction, then this force will have a minus sign. However, when calculating, it is important to know what kind of force this rod is calculated for. For tensile rods, the principle of determining the required section is the simplest:

When designing compression bars, many different factors must be taken into account, and in general view the formula for calculating the compressed rods can be expressed as follows:

σ = N/φF ≤ R

Note: the design scheme can be drawn up so that all longitudinal forces are directed from cross sections. In this case, the "-" sign in front of the force value obtained in the calculations will show that the given rod is in compression.

So the results of the previous calculation show that tensile stresses arise in rods 2-a and 3-b, and compressive forces occur in rods 1-a and a-b. Well, now let's return to the purpose of our calculation - to determine the maximum normal stresses in the rods. As in a conventional symmetrical beam, in which the maximum stresses under a symmetrical load occur in the section furthest from the supports, in the truss the maximum stresses occur in the rods furthest from the supports, i.e. in rods cut off by section IX-IX.

section IX-IX (Fig. 272.2. d)

M 9 \u003d -4.5Q / 2 - 3.5Q - 2.5Q - ​​1.5Q -0.5Q + 3V A - 4.5N 6-w sinα = 0 ;

N 6-z \u003d (15Q - 10.25Q) / (4.5sinα ) = 4.75 190/(4.5 0.158) = 1269.34 kg(works in compression)

where VA = 5Q, the support reactions of the trusses are determined according to the same equilibrium equations of the system, since the truss and loads are symmetrical, then

V A = ΣQ y /2 = 5Q;

since we have not yet provided for horizontal loads, the horizontal support reaction on the support BUT will be equal to zero, so H A is shown in Figure 272.2 b) in light purple.

the shoulders of all forces in this case are different, and therefore the numerical values ​​​​of the shoulders are immediately substituted into the formula.

To determine the force in the rod z-i, you must first determine the value of the angle γ (not shown in the figure). Based on the fact that two sides of a certain right-angled triangle are known (the lower leg or the length of the triangle is 0.5 m, the side leg or the height of the triangle is 0.8 m, then tgγ = 0.8 / 0.5 = 1.6 and the value of the angle γ = arctgγ = 57.99 o. And then for point 3

h = 3sinγ = 2.544 m. Then:

M 3 \u003d - 1.5Q / 2 - 0.5Q + 0.5Q + 1.5Q + 2.5Q - ​​1.5N 6-w sinα + 2.544N = 0 ;

N z-and \u003d (1.25Q - 4.5Q +1.5N 6-s sinα ) /2.544 = (332.5 - 617.5)/2.544 = -112 kg

And now it's easier to formulate the equation of forces about the axis X :

ΣQ x = - N 6-s cosα - N s-and cos γ + N 1-i = 0;

N 1-i \u003d N 6-o cosα + N s-and cosγ = 1269.34 0.987 - 112 0.53 = 1193.46 kg(works in tension)

Since the upper and lower belts of the truss will be from the same type of profile, there is no need to spend time and effort on calculating the rods of the lower belt 1-c, 1-d and 1-g, as well as the rods of the upper belt 4-d and 5-e . The forces in these rods will be clearly less than those already determined by us. If the farm were consoleless, i.e. the supports were located at the ends of the truss, then the forces in the braces would also be less than those already determined by us, however, we have a truss with consoles and therefore we will use several more sections to determine the forces in the braces according to the above algorithm (calculation details are not given):

N b-c \u003d -1527.34 kg - works in compression (section III-III, Fig. 272.2 g), determined by the equation of moments relative to point 1)

N v-g \u003d 634.43 kg - works in tension (section IV-IV, Fig. 272.2 h), determined by the equation of moments relative to point 1)

N g-d \u003d - 493.84 kg - works in compression (section V-V, determined by the equation of moments relative to point 1)

Thus, the most loaded we have are two rods N 6-z \u003d 1269.34 kg and N b-c \u003d - 1527.34 kg. Both rods work in compression, and if the entire truss is made from the same type of profile, then it is enough to calculate one of these rods for ultimate stresses and, based on these calculations, select the required profile section. However, everything is not so simple here, at first glance it seems that it is enough to calculate the rod N b-c, but when calculating the compressed elements great importance has an estimated length of the rod. So the length of the rod N 6-z is 101.2 cm, while the length of the rod N b-c is 59.3 cm. Therefore, in order not to guess, it is better to calculate both rods.

rod N b-z

The calculation of compressed rods is no different from the calculation of centrally compressed columns, therefore, only the main stages of the calculation are given below without detailed explanations.

according to table 1 (see the link above) we determine the value μ = 1 (despite the fact that the upper chord of the truss will be from a solid profile, the calculation scheme of the truss implies the hinged fastening of the rods in the nodes of the truss, so it would be more correct to accept the above value of the coefficient).

We take a preliminary value λ = 90, then according to table 2, the bending coefficient φ \u003d 0.625 (for steel C235 with strength R y \u003d 2350 kgf / cm 2, determined by interpolation of values ​​2050 and 2450)

Then the required radius of gyration will be:

• Choosing a farm scheme
• Triangular structures
• How to calculate the rafter system?
• How to make farms on your own?
  • Buildings made of steel and reinforced concrete
• How to install such farms?

The stability of the manufactured roofs will depend on the quality of its supporting structure, which is based on a truss truss. This product must withstand significant loads, which consist of the weight of the roof cake, as well as the mass of snow that accumulates in winter period time. Strong wind also has an effect. Farms are needed in order to distribute the load that is transferred to the roof and walls of the building. This structure is made in most cases of wood, but there are other options.

For the construction of farms, you can use slats, bars or round timber. To fasten some parts of trusses from bars, you can use the cutting method, and if the elements are made of slats, you will need to use nails or bolts.

In the process of building large buildings with a span of more than 16 m, modern craftsmen use trusses that have stretched metal racks. When using such parts made of wood, it is problematic to fasten knots, so it is allowed to use only metal parts.

A wooden truss truss requires significant labor costs during installation. If you build a combined farm, then the construction process will be much faster.

In most cases, during the construction of residential buildings, the method of erecting a roof with open elements is not used.

Choosing a farm scheme

Figure 1. Scheme of a triangular truss truss.

The choice of the form of the structure must be made based on the following factors:

• material used for coating;
• type of fastening of truss parts;
• detail layout.

If a flat roof is to be arranged, the slope of which does not exceed 12 °, then the truss should be rectangular or trapezoidal.

With more significant slopes of the roof and coverings with a large weight, it is necessary to use triangular-shaped products.

• for a triangular design - 1/5 * L;
• for a rectangular building - 1/6 * L, where L is the length of the truss span.

In most cases, a truss truss in the shape of a triangle is used in construction. The choice of the shape of the rafters will depend on how the trusses will be fixed to the walls of the building. If you combine a construction truss with sloped rafters, it will be possible to create single-slope or double-slope buildings with a different slope.

To achieve the desired stability of a single-slope truss, you will need to install binding devices for several belts. Links can be made from wooden slats, they must be placed at the base of the B-pillar. An ordinary triangular truss is shown in fig. one.

Figure 2. Roof truss installation options.

Items to prepare:

• metal racks;
• wooden bars;
• bolts;
• plumb;
• device for welding;
• metal corners;
• antiseptics;
• profile tubes;
• staples.

Back to index

Triangular structures

The simplest structure is used for private houses with a span of less than 6 m, in which there is no internal load-bearing wall. In this case, the farm will rely solely on the walls of the building from the outside. Such a farm consists of the following elements: rafters, puffs and 2 struts. If the span exceeds 6 m, then you will need to install struts and a part for support. Puffs, which are fixed on trusses, in most cases make it difficult to move around the attic.

As supporting elements, not the walls of the building, but a specially mounted bar are most often used. The only exceptions are buildings made of logs, during the construction of which a bar for support will not be used, since its functions will be performed by the upper crown of the log house. If the building is being built of reinforced concrete, then the installation of a truss truss is a prerequisite. The task of such a design is to evenly distribute the load on the walls. Rafter trusses are durable structures that are constructed from metal. Farm parts are fastened with bolts. Another option is to use a welding device. In exceptional cases, reinforced concrete products are used.

Back to index

How to calculate the rafter system?

To calculate the rafter system, you will need to take into account all the loads that will be transferred to the rafters.

Loads are divided into the following types:

1. Continuous (pie weight roofing).
2. Temporary (wind load, snow weight, people who climb the roof to perform repairs).
3. Special. Seismic load can be attributed to this type, for example.

The determination of the snow load must be carried out on the basis of climatic conditions a certain region. You will need to use the following formula: S \u003d Sg * u, where u is a coefficient that depends on the roof slope, and Sg is the calculated indicator of the weight of the snow load per 1 m² of coverage. This parameter must be determined from the tables. In the process of determining the wind load, the following indicators should be taken into account:

1. Structure height.
2. Terrain type.
3. Normative value of wind load.

The necessary tables and calculation formulas can be found in building codes. In most cases, these calculations are made by designers. If you plan to calculate the farm yourself, then you need to know that the slightest mistake can lead to the roof system being unreliable.

Back to index

How to make farms on your own?

Previously, farms of this type were built on construction sites, but today such structures are manufactured in the factory.

Production of farms is carried out on special equipment.

If wooden structures are made, then they must be treated with protective agents that can prevent rotting.

Thanks to the application the latest technologies you can build products of this type for roofs of various shapes.

It is possible to manufacture both complete trusses and their individual parts, which will later be assembled into a single structure at the construction site.

Back to index

Buildings made of steel and reinforced concrete

In private construction, steel buildings are often used. Farm types can be as follows:

• triangular;
• polygonal;
• with multiple belts.

If the plans include the construction of a soft roof, then the last two types of trusses can be used. For sheet materials, triangular-shaped products are suitable. In industrial conditions, steel structures are manufactured in standard sizes, which are suitable for spans with a length of 18, 24 and 36 m.

Truss belts and lattices are made of metal corners. Rational is the construction, the belts of which are constructed from wide-shelf beams. Such structures are easy to manufacture. To build such elements, you need only a small amount of materials. However, the products are durable and reliable.

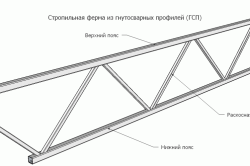
The truss truss made of steel differs from the truss truss by the presence of an additional belt. They have standard sizes. In the process of erecting private houses, in most cases, steel products are used, which are constructed from rectangular profile tubes. Such structures are lighter than products that are constructed from a metal corner.

A similar structure can be built on the construction site using a welding device.

In modern construction work reinforced concrete trusses are also used. Such trusses are best mounted on the roofs of buildings of low height, which experience significant loads on the coatings. Farms from this material can be divided into:

1. Diagonal and non-diagonal products.
2. Designs for roofs with a slight slope.
3. triangular structures.

In the construction of residential buildings, reinforced concrete products are rarely used. The disadvantages of such farms include considerable weight and complexity of installation.