Úhel mezi dvěma přímkami v prostoru. Nejjednodušší úlohy s přímkou ​​na rovině

ÚHEL MEZI ROVINAMI

Uvažujme dvě roviny α 1 a α 2 definované rovnicemi:

Pod úhel mezi dvěma rovinami budeme rozumět jednomu z dihedrálních úhlů tvořených těmito rovinami. Je zřejmé, že úhel mezi normálovými vektory a rovinami α 1 a α 2 je roven jednomu z naznačených sousedních dihedrálních úhlů popř. . Proto . Protože A , Že

.

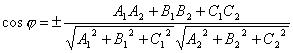Příklad. Určete úhel mezi rovinami X+2y-3z+4=0 a 2 X+3y+z+8=0.

Podmínka pro rovnoběžnost dvou rovin.

Dvě roviny α 1 a α 2 jsou rovnoběžné právě tehdy, když jsou jejich normálové vektory rovnoběžné, a proto .

Dvě roviny jsou tedy navzájem rovnoběžné právě tehdy, když koeficienty odpovídajících souřadnic jsou úměrné:

nebo

Podmínka kolmosti rovin.

Je jasné, že dvě roviny jsou kolmé právě tehdy, když jsou jejich normálové vektory kolmé, a proto, nebo .

Tím pádem, .

Příklady.

PŘÍMO V PROSTORU.

VEKTOROVÁ ROVNICE PRO ČÁRU.

PARAMETRICKÉ PŘÍMÉ ROVNICE

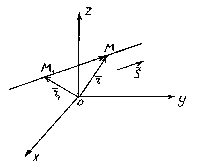
Poloha čáry v prostoru je zcela určena určením libovolného z jejích pevných bodů M 1 a vektor rovnoběžný s touto přímkou.

Nazývá se vektor rovnoběžný s přímkou průvodci vektor této čáry.

Nechte tedy rovnou čáru l prochází bodem M 1 (X 1 , y 1 , z 1), ležící na přímce rovnoběžné s vektorem .

Zvažte libovolný bod M(x,y,z) na přímce. Z obrázku je zřejmé, že .

Vektory a jsou kolineární, takže existuje takové číslo t, co , kde je násobitel t může nabývat libovolné číselné hodnoty v závislosti na poloze bodu M na přímce. Faktor t nazývaný parametr. Po určení poloměrových vektorů bodů M 1 a M respektive prostřednictvím a , získáme . Tato rovnice se nazývá vektor rovnice přímky. Ukazuje, že pro každý parametr hodnotu t odpovídá vektoru poloměru nějakého bodu M, ležící na přímce.

Zapišme tuto rovnici v souřadnicovém tvaru. Všimněte si, že, a odtud

Výsledné rovnice se nazývají parametrické rovnice přímky.

Při změně parametru t změna souřadnic X, y A z a tečka M se pohybuje v přímé linii.

KANONICKÉ ROVNICE PŘÍMÉ

Nechat M 1 (X 1 , y 1 , z 1) – bod ležící na přímce l, A je jeho směrový vektor. Vezměme opět libovolný bod na přímce M(x,y,z) a zvažte vektor .

Je jasné, že vektory jsou také kolineární, takže jejich odpovídající souřadnice musí být úměrné,

– kanonický rovnice přímky.

Poznámka 1. Všimněte si, že kanonické rovnice přímky lze získat z parametrických eliminací parametru t. Ve skutečnosti z parametrických rovnic, které získáme nebo .

Příklad. Zapište rovnici přímky v parametrické podobě.

Označme , odtud X = 2 + 3t, y = –1 + 2t, z = 1 –t.

Poznámka 2 Nechť je přímka kolmá k jedné ze souřadnicových os, například k ose Vůl. Potom je směrový vektor přímky kolmý Vůl, tedy, m=0. V důsledku toho budou mít parametrické rovnice přímky tvar

Vyloučení parametru z rovnic t, získáme rovnice přímky ve tvaru

I v tomto případě však souhlasíme s formálním psaním kanonické rovnice rovnou ve formě . Pokud je tedy jmenovatel jednoho ze zlomků nulový, znamená to, že přímka je kolmá k příslušné souřadnicové ose.

Podobně jako u kanonických rovnic odpovídá přímce kolmé k osám Vůl A Oj nebo rovnoběžně s osou Oz.

Příklady.

OBECNÉ ROVNICE PŘÍMKY JAKO ČÁRY KŘÍŽENÍ DVOU ROVIN

Každou přímkou ​​v prostoru prochází nespočet rovin. Jakékoli dva z nich, které se protínají, jej definují v prostoru. V důsledku toho rovnice jakýchkoli dvou takových rovin, uvažované společně, představují rovnice této přímky.

Obecně jakékoli dvě nerovnoběžné roviny dané obecnými rovnicemi

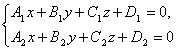
určit přímku jejich průsečíku. Tyto rovnice se nazývají obecné rovnice rovný.

Příklady.

Sestrojte přímku danou rovnicí

K sestrojení přímky stačí najít dva její body. Nejjednodušší způsob je vybrat průsečíky přímky s souřadnicové roviny. Například průsečík s rovinou xOy získáme z rovnic přímky za předpokladu z= 0:

Po vyřešení tohoto systému najdeme pointu M 1 (1;2;0).

Podobně za předpokladu y= 0, dostaneme průsečík přímky s rovinou xOz:

Od obecných rovnic přímky lze přejít k jejím kanonickým nebo parametrickým rovnicím. Chcete-li to provést, musíte najít nějaký bod M 1 na přímce a směrový vektor přímky.

Souřadnice bodu M 1 získáme z tohoto systému rovnic, přičemž jedné ze souřadnic přiřadíme libovolnou hodnotu. Chcete-li najít směrový vektor, poznamenejte si, že tento vektor musí být kolmý k oběma normálovým vektorům A . Tedy mimo směrový vektor přímky l můžete vzít vektorový součin normálních vektorů:

.

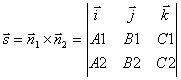Příklad. Uveďte obecné rovnice přímky na kanonickou formu.

Najdeme bod ležící na přímce. K tomu zvolíme libovolně jednu ze souřadnic, např. y= 0 a vyřeš soustavu rovnic:

Normální vektory rovin definujících přímku mají souřadnice Proto bude směrový vektor přímý

. Proto, l: .

ÚHEL MEZI PŘÍMKAMI

Úhel mezi přímkami v prostoru budeme nazývat libovolný ze sousedních úhlů tvořených dvěma přímkami vedenými libovolným bodem rovnoběžným s daty.

Nechť jsou v prostoru uvedeny dvě čáry:

Je zřejmé, že úhel φ mezi přímkami lze brát jako úhel mezi jejich směrovými vektory a . Od , pak pomocí vzorce pro kosinus úhlu mezi vektory dostaneme

Instrukce

Poznámka

Doba goniometrická funkce Tangenta je rovna 180 stupňům, což znamená, že úhly sklonu přímek nemohou v absolutní hodnotě překročit tuto hodnotu.

Užitečná rada

Pokud jsou úhlové koeficienty navzájem stejné, pak úhel mezi takovými čarami je 0, protože takové čáry se buď shodují, nebo jsou rovnoběžné.

Pro určení hodnoty úhlu mezi protínajícími se úsečkami je nutné obě úsečky (nebo jednu z nich) posunout do nové polohy metodou paralelního posunu, dokud se neprotnou. Poté byste měli najít úhel mezi výslednými protínajícími se čarami.

Budete potřebovat

• Pravítko, pravoúhlý trojuhelník, tužka, úhloměr.

Instrukce

Nechť je tedy dán vektor V = (a, b, c) a rovina A x + B y + C z = 0, kde A, B a C jsou souřadnice normály N. Potom kosinus úhlu α mezi vektory V a N se rovná: cos α = (a A + b B + c C)/(√(a² + b² + c²) √(A² + B² + C²)).

Pro výpočet úhlu ve stupních nebo radiánech je potřeba z výsledného výrazu vypočítat inverzní funkci ke kosinusu, tzn. arkosin:α = аrsсos ((a A + b B + c C)/(√(a² + b² + c²) √(A² + B² + C²))).

Příklad: najít roh mezi vektor(5, -3, 8) a letadlo, daný obecná rovnice 2 x – 5 y + 3 z = 0. Řešení: zapište souřadnice normálového vektoru roviny N = (2, -5, 3). Dosaďte všechny známé hodnoty do uvedeného vzorce: cos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.

Video k tématu

Přímka, která má jeden společný bod s kružnicí, je tečnou ke kružnici. Dalším znakem tečny je, že je vždy kolmá k poloměru nakreslenému k bodu dotyku, to znamená, že tečna a poloměr tvoří přímku. roh. Jsou-li dvě tečny ke kružnici AB a AC vedeny z jednoho bodu A, pak jsou si vždy rovny. Určení úhlu mezi tečnami ( roh ABC) se vyrábí pomocí Pythagorovy věty.

Instrukce

Pro určení úhlu potřebujete znát poloměr kružnice OB a OS a vzdálenost počátečního bodu tečny od středu kružnice - O. Úhly ABO a ACO jsou tedy stejné, poloměr OB je, například 10 cm a vzdálenost ke středu kružnice AO je 15 cm Délku tečny určete pomocí vzorce podle Pythagorovy věty: AB = Odmocnina od AO2 – OB2 nebo 152 - 102 = 225 – 100 = 125;

Nechť jsou v prostoru uvedeny rovné čáry l A m. Přes nějaký bod A prostoru kreslíme rovné čáry l 1 || l A m 1 || m(obr. 138).

Všimněte si, že bod A může být zvolen libovolně, zejména může ležet na jedné z těchto přímek. Pokud rovnou l A m protínají, pak lze A považovat za průsečík těchto čar ( l 1 = l A m 1 = m).

Úhel mezi nerovnoběžnými čarami l A m je hodnota nejmenšího ze sousedních úhlů tvořených protínajícími se přímkami l 1 A m 1 (l 1 || l, m 1 || m). Úhel mezi rovnoběžnými čarami se považuje za rovný nule.

Úhel mezi přímkami l A m označeno \(\widehat((l;m))\). Z definice vyplývá, že pokud se měří ve stupních, pak 0° < \(\widehat((l;m)) \) < 90°, a pokud v radiánech, pak 0 < \(\widehat((l;m)) \) < π / 2 .

Úkol. Je dána krychle ABCDA 1 B 1 C 1 D 1 (obr. 139).

Najděte úhel mezi přímkami AB a DC 1.

Přímky AB a DC 1 křížení. Protože přímka DC je rovnoběžná s přímkou ​​AB, úhel mezi přímkami AB a DC 1 je podle definice roven \(\widehat(C_(1)DC)\).

Proto \(\widehat((AB;DC_1))\) = 45°.

Přímo l A m jsou nazývány kolmý, jestliže \(\widehat((l;m)) \) = π / 2. Například v krychli

Výpočet úhlu mezi přímkami.

Problém výpočtu úhlu mezi dvěma přímkami v prostoru je řešen stejně jako v rovině. Označme φ velikost úhlu mezi úsečkami l 1 A l 2 a skrz ψ - velikost úhlu mezi směrovými vektory A A b tyto rovné čáry.

Pak pokud

ψ <90° (рис. 206, а), то φ = ψ; если же ψ >90° (obr. 206.6), pak φ = 180° - ψ. Je zřejmé, že v obou případech platí rovnost cos φ = |cos ψ|. Podle vzorce (kosinus úhlu mezi nenulovými vektory a a b se rovná skalárnímu součinu těchto vektorů dělenému součinem jejich délek) máme

$$ cos\psi = cos\widehat((a; b)) = \frac(a\cdot b)(|a|\cdot |b|) $$

proto,

$$ cos\phi = \frac(|a\cdot b|)(|a|\cdot |b|) $$

Nechť jsou přímky dány jejich kanonickými rovnicemi

$$ \frac(x-x_1)(a_1)=\frac(y-y_1)(a_2)=\frac(z-z_1)(a_3) \;\; A \;\; \frac(x-x_2)(b_1)=\frac(y-y_2)(b_2)=\frac(z-z_2)(b_3) $$

Potom se pomocí vzorce určí úhel φ mezi přímkami

$$ cos\phi = \frac(|a_(1)b_1+a_(2)b_2+a_(3)b_3|)(\sqrt((a_1)^2+(a_2)^2+(a_3)^2 )\sqrt((b_1)^2+(b_2)^2+(b_3)^2)) (1)$$

Pokud je jedna z čar (nebo obě) dána nekanonickými rovnicemi, pak pro výpočet úhlu musíte najít souřadnice směrových vektorů těchto čar a poté použít vzorec (1).

Úkol 1. Vypočítejte úhel mezi čarami

$$ \frac(x+3)(-\sqrt2)=\frac(y)(\sqrt2)=\frac(z-7)(-2) \;\;and\;\; \frac(x)(\sqrt3)=\frac(y+1)(\sqrt3)=\frac(z-1)(\sqrt6) $$

Směrové vektory přímek mají souřadnice:

a = (-√2; √2; -2), b = (√3 ; √3 ; √6 ).

Pomocí vzorce (1) najdeme

$$ cos\phi = \frac(|-\sqrt6+\sqrt6-2\sqrt6|)(\sqrt(2+2+4)\sqrt(3+3+6))=\frac(2\sqrt6)( 2\sqrt2\cdot 2\sqrt3)=\frac(1)(2) $$

Proto je úhel mezi těmito čarami 60°.

Úkol 2. Vypočítejte úhel mezi čarami

$$ \začátek(případy)3x-12z+7=0\\x+y-3z-1=0\konec (případy) a \začátek(případy)4x-y+z=0\\y+z+1 =0\end(cases) $$

Za vodicím vektorem A Na prvním řádku vezmeme vektorový součin normálních vektorů n 1 = (3; 0; -12) a n 2 = (1; 1; -3) roviny definující tuto přímku. Pomocí vzorce \(=\begin(vmatrix) i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end(vmatrix) \) dostaneme

$$ a==\begin(vmatrix) i & j & k \\ 3 & 0 & -12 \\ 1 & 1 & -3 \end(vmatrix)=12i-3i+3k $$

Podobně najdeme směrový vektor druhé přímky:

$$ b=\začátek(vmatice) i & j & k \\ 4 & -1 & 1 \\ 0 & 1 & 1 \end(vmatice)=-2i-4i+4k $$

Ale pomocí vzorce (1) vypočítáme kosinus požadovaného úhlu:

$$ cos\phi = \frac(|12\cdot (-2)-3(-4)+3\cdot 4|)(\sqrt(12^2+3^2+3^2)\sqrt(2 ^2+4^2+4^2))=0 $$

Proto je úhel mezi těmito čarami 90°.

Úkol 3. V trojúhelníková pyramida MABC žebra MA, MB a MS jsou vzájemně kolmá (obr. 207);

jejich délky jsou 4, 3, 6. Bod D je střed [MA]. Najděte úhel φ mezi přímkami CA a DB.

Nechť CA a DB jsou směrové vektory přímek CA a DB.

Vezměme bod M jako počátek souřadnic. Podle podmínky rovnice máme A (4; 0; 0), B(0; 0; 3), C(0; 6; 0), D (2; 0; 0). Proto \(\overrightarrow(CA)\) = (4; - 6;0), \(\overrightarrow(DB)\)= (-2; 0; 3). Použijeme vzorec (1):

$$ cos\phi=\frac(|4\cdot (-2)+(-6)\cdot 0+0\cdot 3|)(\sqrt(16+36+0)\sqrt(4+0+9 )) $$

Pomocí cosinové tabulky zjistíme, že úhel mezi přímkami CA a DB je přibližně 72°.

Úhel mezi přímkami v prostoru budeme nazývat libovolný ze sousedních úhlů tvořených dvěma přímkami vedenými libovolným bodem rovnoběžným s daty.

Nechť jsou v prostoru uvedeny dvě čáry:

Je zřejmé, že úhel φ mezi přímkami lze brát jako úhel mezi jejich směrovými vektory a . Od , pak pomocí vzorce pro kosinus úhlu mezi vektory dostaneme

Podmínky rovnoběžnosti a kolmosti dvou přímek jsou ekvivalentní podmínkám rovnoběžnosti a kolmosti jejich směrových vektorů a:

Dvě rovné paralelní právě tehdy, jsou-li jim odpovídající koeficienty poměrné, tzn. l 1 paralelní l 2 právě tehdy, když jsou rovnoběžné .

Dvě rovné kolmý právě tehdy, je-li součet součinů odpovídajících koeficientů roven nule: .

U cíl mezi přímkou ​​a rovinou

Ať je to rovné d- není kolmá k rovině θ;
d′− projekce přímky d k rovině 9;
Nejmenší úhel mezi přímkami d A d"zavoláme úhel mezi přímkou ​​a rovinou.
Označme to jako φ=( d,θ)
Li d⊥θ, pak ( d,θ)=π/2

Oi→j→k→− pravoúhlý souřadnicový systém.
Rovinná rovnice:

θ: Sekera+Podle+Cz+D=0

Předpokládáme, že přímka je definována bodem a směrovým vektorem: d[M 0,p→]
Vektor n→(A,B,C)⊥θ
Pak zbývá zjistit úhel mezi vektory n→ a p→, označme to jako γ=( n→,p→).

Pokud úhel γ<π/2 , то искомый угол φ=π/2−γ .

Pokud je úhel γ>π/2, pak požadovaný úhel je φ=γ−π/2

sinφ=sin(2π−γ)=cosγ

sinφ=sin(γ−2π)=−cosγ

Pak, úhel mezi přímkou ​​a rovinou lze vypočítat pomocí vzorce:

sinφ=∣cosγ∣=∣ ∣ Ap 1+Bp 2+Cp 3∣ ∣ √A 2+B 2+C 2√p 21+p 22+p 23

Otázka 29. Pojem kvadratické formy. Znaménková určitost kvadratických forem.

Kvadratický tvar j (x 1, x 2, …, x n) n reálných proměnných x 1, x 2, …, x n se nazývá součet tvaru
, (1)

Kde a ij – některá čísla nazývaná koeficienty. Bez ztráty obecnosti to můžeme předpokládat a ij = a ji.

Kvadratická forma se nazývá platný, Li a ij Î GR. Matice kvadratického tvaru se nazývá matice složená z jejích koeficientů. Kvadratický tvar (1) odpovídá jediné symetrické matici
To znamená A T = A. V důsledku toho lze kvadratickou formu (1) zapsat v maticovém tvaru j ( X) = x T Ah, Kde x T = (X 1 X 2 … x n). (2)

A naopak každá symetrická matice (2) odpovídá jedinečné kvadratické formě až po zápis proměnných.

Hodnost kvadratické formy se nazývá hodnost jeho matice. Kvadratická forma se nazývá nedegenerovaný, pokud jeho matice není singulární A. (připomeňme, že matrice A se nazývá nedegenerovaný, pokud jeho determinant není roven nule). Jinak je kvadratická forma degenerovaná.

pozitivní definitivní(nebo přísně pozitivní), pokud

j( X) > 0 , pro každého X = (X 1 , X 2 , …, x n), až na X = (0, 0, …, 0).

Matice A kladně určitý kvadratický tvar j ( X) se také nazývá pozitivně určitý. Proto kladně definitní kvadratická forma odpovídá jedinečné pozitivně definitní matici a naopak.

Kvadratická forma (1) se nazývá negativně definované(nebo přísně negativní), pokud

j( X) < 0, для любого X = (X 1 , X 2 , …, x n), až na X = (0, 0, …, 0).

Podobně jako výše, matice záporně definitní kvadratické formy se také nazývá negativně definitní.

V důsledku toho kladná (záporná) určitá kvadratická forma j ( X) dosáhne minimální (maximální) hodnoty j ( X*) = 0 at X* = (0, 0, …, 0).

Všimněte si, že většina kvadratických forem není znaménko-definitivní, to znamená, že nejsou ani pozitivní, ani negativní. Takové kvadratické formy mizí nejen v počátku souřadnicového systému, ale také v jiných bodech.

Když n> 2, jsou vyžadována speciální kritéria pro kontrolu znaménka kvadratické formy. Pojďme se na ně podívat.

Hlavní nezletilí kvadratické formy se nazývají nezletilé:

to znamená, že se jedná o nezletilé v řádu 1, 2, ..., n matrice A, umístěný v levém horním rohu, poslední z nich se shoduje s determinantem matice A.

Pozitivní kritérium jednoznačnosti (Sylvesterovo kritérium)

X) = x T Ah byl kladně definitivní, je nutné a postačující, aby všechny hlavní nezletilé matice A byly pozitivní, tedy: M 1 > 0, M 2 > 0, …, Mn > 0. Negativní kritérium jistoty Aby kvadratická forma j ( X) = x T Ah byl záporně určitý, je nutné a postačující, aby jeho hlavní minority sudého řádu byly kladné a lichého řádu - záporné, tj.: M 1 < 0, M 2 > 0, M 3 < 0, …, (–1)n

Označíme-li na přímce v prostoru dva libovolné body M 1 (x 1, y 1, z 1) a M 2 (x 2, y 2, z 2), pak musí souřadnice těchto bodů splňovat rovnici přímky získané výše:

Navíc pro bod M 1 můžeme napsat:

.

Když tyto rovnice vyřešíme společně, dostaneme:

.

Toto je rovnice přímky procházející dvěma body v prostoru.

Obecné rovnice přímky v prostoru.

Rovnici přímky lze považovat za rovnici průsečíku dvou rovin.

Obecné rovnice přímky v souřadnicovém tvaru:

Praktickým úkolem je často redukovat rovnice přímek na obecný pohled na kanonickou formu.

Chcete-li to provést, musíte najít libovolný bod na přímce a čísla m, n, p.

V tomto případě lze směrový vektor přímky nalézt jako vektorový součin normálových vektorů k daným rovinám.

Příklad. Najděte kanonickou rovnici, pokud je přímka uvedena ve tvaru:

Abychom našli libovolný bod na přímce, vezmeme jeho souřadnici x = 0 a dosadíme tuto hodnotu do daného systému rovnic.

Tito. A(0; 2; 1).

Najděte složky směrovacího vektoru přímky.

Potom kanonické rovnice přímky:

Příklad. Uveďte do kanonické podoby rovnici přímky ve tvaru:

Abychom našli libovolný bod na přímce, která je průsečíkem výše uvedených rovin, vezmeme z = 0. Pak:

;

2x – 9x – 7 = 0;

Dostaneme: A(-1; 3; 0).

Přímý vektor: .

Úhel mezi rovinami.

Úhel mezi dvěma rovinami v prostoru  souvisí s úhlem mezi normálami k těmto rovinám  1 vztahem:  =  1 nebo  = 180 0 -  1, tzn.

cos = cos 1 .

Určíme úhel  1. Je známo, že roviny lze specifikovat pomocí vztahů:

, Kde

(A1, B1, C1), (A2, B2, C2). Najdeme úhel mezi normálovými vektory z jejich skalárního součinu:

.

Úhel mezi rovinami se tedy najde podle vzorce:

Volba znaménka kosinusu závisí na tom, jaký úhel mezi rovinami by měl být nalezen - ostrý nebo přilehlý k němu tupý.

Podmínky rovnoběžnosti a kolmosti rovin.

Na základě výše získaného vzorce pro nalezení úhlu mezi rovinami lze najít podmínky pro rovnoběžnost a kolmost rovin.

Aby byly roviny kolmé, je nutné a postačující, aby kosinus úhlu mezi rovinami byl roven nule. Tato podmínka je splněna, pokud:

Roviny jsou rovnoběžné, normálové vektory jsou kolineární:  .Tato podmínka je splněna, pokud: .

Úhel mezi přímkami v prostoru.

Nechť jsou v prostoru uvedeny dvě čáry. Jejich parametrické rovnice jsou:

Úhel mezi přímkami  a úhel mezi směrovými vektory  těchto přímek souvisí vztahem:  =  1 nebo  = 180 0 -  1. Úhel mezi směrovými vektory se zjistí ze skalárního součinu. Tím pádem:

.

Podmínky rovnoběžnosti a kolmosti přímek v prostoru.

Aby byly dvě přímky rovnoběžné, je nutné a postačující, aby směrové vektory těchto přímek byly kolineární, tzn. jejich odpovídající souřadnice byly úměrné.