Proprietățile diagonalelor unui paralelogram. Lecții complete – Knowledge Hypermarket

În lecția de astăzi vom trece în revistă proprietățile de bază ale unui paralelogram, apoi vom acorda atenție luării în considerare a primelor două proprietăți ale unui paralelogram și le vom demonstra. În cursul demonstrației, să ne amintim utilizarea testelor pentru egalitatea triunghiurilor, pe care le-am studiat anul trecut și le-am repetat în prima lecție. La final se va da un exemplu de aplicare a caracteristicilor studiate ale unui paralelogram.

Subiect: Cadrilatere

Lecția: Semne ale unui paralelogram

Să începem prin a aminti definiția paralelogramului.

Definiţie. Paralelogram- un patrulater în care fiecare două laturi opuse sunt paralele (vezi Fig. 1).

Orez. 1. Paralelogram

Să ne amintim proprietățile de bază ale paralelogramului:

Pentru a putea folosi toate aceste proprietăți, trebuie să fii sigur că figura în cauză este un paralelogram. Pentru a face acest lucru, trebuie să cunoașteți fapte precum caracteristicile unui paralelogram. Le vom lua în considerare astăzi pe primele două dintre ele.

Teorema. Primul semn al paralelogramului. Dacă două laturi opuse ale unui patrulater sunt egale și paralele, atunci acest patrulater este paralelogram. .

Orez. 2. Primul semn al unui paralelogram

Dovada. Să desenăm o diagonală în patrulater (vezi Fig. 2), o împarte în două triunghiuri. Să scriem ce știm despre aceste triunghiuri:

după primul criteriu de egalitate a triunghiurilor.

Din egalitatea triunghiurilor indicate rezultă că în virtutea paralelismului dreptelor când se intersectează cu o secante. Avem asta:

Dovedit.

Teorema. Al doilea semn al unui paralelogram. Dacă într-un patrulater fiecare două laturi opuse sunt egale, atunci acest patrulater este paralelogram. .

Orez. 3. Al doilea semn al unui paralelogram

Dovada. Să desenăm o diagonală în patrulater (vezi Fig. 3), o împarte în două triunghiuri. Să scriem ce știm despre aceste triunghiuri pe baza formulării teoremei:

conform celui de-al treilea criteriu pentru egalitatea triunghiurilor.

Din egalitatea triunghiurilor rezultă că prin principiul paralelismului dreptelor atunci când acestea se intersectează cu o secante. Primim:

paralelogram prin definiție. Q.E.D.

Dovedit.

Să ne uităm la un exemplu de utilizare a caracteristicilor paralelogramului.

Exemplul 1. Într-un patrulater convex Aflați: a) unghiurile patrulaterului; b) lateral.

Soluţie. Să reprezentăm Fig. 4.

Orez. 4

paralelogram după primul semn al paralelogramului.

Un paralelogram este un patrulater ale cărui laturi opuse sunt paralele în perechi (Fig. 233).

Pentru un paralelogram arbitrar sunt valabile următoarele proprietăți:

1. Laturile opuse ale unui paralelogram sunt egale.

Dovada. În paralelogramul ABCD desenăm diagonala AC. Triunghiurile ACD și AC B sunt egale, având o latură comună AC și două perechi de unghiuri egale adiacente acesteia:

(ca unghiurile transversale cu drepte paralele AD și BC). Aceasta înseamnă, la fel ca laturile triunghiurilor egale situate opuse unghiurilor egale, ceea ce trebuia demonstrat.

2. Unghiurile opuse ale unui paralelogram sunt egale:

3. Unghiurile adiacente ale unui paralelogram, adică unghiurile adiacente unei laturi, se adună etc.

Dovada proprietăților 2 și 3 se obține imediat din proprietățile unghiurilor pentru drepte paralele.

4. Diagonalele unui paralelogram se bisectează în punctul lor de intersecție. Cu alte cuvinte,

Dovada. Triunghiurile AOD și BOC sunt congruente, deoarece laturile lor AD și BC sunt egale (proprietatea 1) și unghiurile adiacente lor (ca unghiurile transversale pentru liniile paralele). De aici rezultă că laturile corespunzătoare acestor triunghiuri sunt egale: AO, care este ceea ce trebuia demonstrat.

Fiecare dintre aceste patru proprietăți caracterizează un paralelogram sau, după cum se spune, este proprietatea sa caracteristică, adică fiecare patrulater care are cel puțin una dintre aceste proprietăți este un paralelogram (și, prin urmare, are toate celelalte trei proprietăți).

Să facem dovada pentru fiecare proprietate separat.

1". Dacă laturile opuse ale unui patrulater sunt egale în perechi, atunci acesta este un paralelogram.

Dovada. Fie patrulaterul ABCD să aibă laturile AD și BC, AB și respectiv CD egale (Fig. 233). Să desenăm diagonala AC. Triunghiuri ABCși CDA va fi egală, având trei perechi de laturi egale.

Dar atunci unghiurile BAC și DCA sunt egale și . Paralelismul laturilor BC și AD rezultă din egalitatea unghiurilor CAD și ACB.

2. Dacă un patrulater are două perechi de unghiuri opuse egale, atunci este un paralelogram.

Dovada. Lasă . De atunci, ambele părți AD și BC sunt paralele (pe baza paralelismului dreptelor).

3. Lăsăm cititorului formularea și dovada.

4. Dacă diagonalele unui patrulater se bisectează în punctul de intersecție, atunci patrulaterul este un paralelogram.

Dovada. Dacă AO = OS, BO = OD (Fig. 233), atunci triunghiurile AOD și BOC sunt egale, ca având unghiuri egale (vertical!) la vârful O, închise între perechi de laturi egale AO și CO, BO și DO. Din egalitatea triunghiurilor concluzionăm că laturile AD și BC sunt egale. Laturile AB și CD sunt de asemenea egale, iar patrulaterul se dovedește a fi un paralelogram conform proprietății caracteristice G.

Astfel, pentru a demonstra că un patrulater dat este un paralelogram, este suficient să verificăm validitatea oricăreia dintre cele patru proprietăți. Cititorul este invitat să demonstreze independent o altă proprietate caracteristică a unui paralelogram.

5. Dacă un patrulater are o pereche de laturi egale, paralele, atunci este un paralelogram.

Uneori, orice pereche de laturi paralele ale unui paralelogram se numește bazele sale, apoi celelalte două sunt numite laturi laterale. Un segment de linie dreaptă perpendicular pe două laturi ale unui paralelogram, închis între ele, se numește înălțimea paralelogramului. Paralelogramul din fig. 234 are o înălțime h trasă pe laturile AD și BC, a doua înălțime a sa este reprezentată de segmentul .

Un paralelogram este un patrulater ale cărui laturi opuse sunt paralele în perechi. Următoarea figură prezintă paralelogramul ABCD. Are latura AB paralelă cu latura CD și latura BC paralelă cu latura AD.

După cum probabil ați ghicit, un paralelogram este un patrulater convex. Să luăm în considerare proprietățile de bază ale unui paralelogram.

Proprietățile unui paralelogram

1. Într-un paralelogram, unghiurile opuse și laturile opuse sunt egale. Să demonstrăm această proprietate - luați în considerare paralelogramul prezentat în figura următoare.

Diagonala BD îl împarte în două triunghiuri egale: ABD și CBD. Ele sunt egale de-a lungul laturii BD și a celor două unghiuri adiacente acesteia, deoarece unghiurile situate transversal la secanta BD a dreptelor paralele BC și AD și, respectiv, AB și CD. Prin urmare AB = CD și
BC = AD. Și din egalitatea unghiurilor 1, 2, 3 și 4 rezultă că unghiul A = unghiul 1 + unghiul 3 = unghiul 2 + unghiul 4 = unghiul C.

2. Diagonalele unui paralelogram se împart la jumătate la punctul de intersecție. Fie punctul O punctul de intersecție al diagonalelor AC și BD ale paralelogramului ABCD.

Atunci triunghiul AOB și triunghiul COD sunt egali unul cu celălalt, de-a lungul laturii și a două unghiuri adiacente. (AB = CD, deoarece acestea sunt laturi opuse ale paralelogramului. Și unghi1 = unghi2 și unghi3 = unghi4 ca unghiuri transversale atunci când dreptele AB și CD se intersectează cu secantele AC și, respectiv, BD.) De aici rezultă că AO = OC și OB = OD, care și trebuia dovedit.

Toate proprietățile principale sunt ilustrate în următoarele trei figuri.

Acesta este un patrulater ale cărui laturi opuse sunt paralele în perechi.

Proprietatea 1. Orice diagonală a unui paralelogram îl împarte în două triunghiuri egale.

Dovada . După caracteristica II (unghiuri transversale și latura comună).

Teorema este demonstrată.

Proprietatea 2. Într-un paralelogram, laturile opuse sunt egale, iar unghiurile opuse sunt egale.

Dovada .
De asemenea,

Teorema este demonstrată.

Proprietatea 3. Într-un paralelogram, diagonalele sunt tăiate în două de punctul de intersecție.

Dovada .

Teorema este demonstrată.

Proprietatea 4. Bisectoarea unghiului unui paralelogram, care intersectează latura opusă, îl împarte în triunghi isoscelși trapez. (Ch. cuvinte - vârf - doi isoscele? -ka).

Dovada .

Teorema este demonstrată.

Proprietatea 5. Într-un paralelogram, un segment de dreaptă cu capete pe laturi opuse care trece prin punctul de intersecție al diagonalelor este tăiat în două de acest punct.

Dovada .

Teorema este demonstrată.

Proprietatea 6. Unghiul dintre înălțimile căzute de la vârful unui unghi obtuz al unui paralelogram este egal cu colț ascuțit paralelogram.

Dovada .

Teorema este demonstrată.

Proprietatea 7. Suma unghiurilor unui paralelogram adiacent unei laturi este de 180°.

Dovada .

Teorema este demonstrată.

Construirea bisectoarei unui unghi. Proprietățile bisectoarei unui triunghi.

1) Construiți o rază arbitrară DE.

2) Pe o rază dată, construiți un cerc arbitrar cu un centru la vârf și același
cu centrul la începutul razei construite.

3) F și G - punctele de intersecție ale cercului cu laturile unui unghi dat, H - punctul de intersecție al cercului cu raza construită

Construiți un cerc cu centrul în punctul H și raza egală cu FG.

5) I este punctul de intersecție al cercurilor grinzii construite.

6) Desenați o linie dreaptă prin vârf și I.

IDH este unghiul necesar.
)

Proprietatea 1. Bisectoarea unui unghi al unui triunghi împarte latura opusă proporțional cu laturile adiacente.

Dovada . Fie x, y segmente ale laturii c. Să continuăm fasciculul BC. Pe raza BC trasăm din C un segment CK egal cu AC.

Conceptul de paralelogram

Definiția 1

Paralelogram este un patrulater în care laturile opuse sunt paralele între ele (Fig. 1).

Figura 1.

Un paralelogram are două proprietăți principale. Să le luăm în considerare fără dovezi.

Proprietatea 1: Laturile și unghiurile opuse ale unui paralelogram sunt egale.

Proprietatea 2: Diagonalele desenate într-un paralelogram sunt tăiate în două de punctul lor de intersecție.

Semne ale unui paralelogram

Să luăm în considerare trei caracteristici ale unui paralelogram și să le prezentăm sub formă de teoreme.

Teorema 1

Dacă două laturi ale unui patrulater sunt egale între ele și, de asemenea, paralele, atunci acest patrulater va fi un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. În care $AB||CD$ și $AB=CD$ Să desenăm în ea o diagonală $AC$ (Fig. 2).

Figura 2.

Luați în considerare liniile paralele $AB$ și $CD$ și secantele lor $AC$. Apoi

\[\angle CAB=\angle DCA\]

ca niște colțuri încrucișate.

Conform criteriului $I$ al egalității triunghiurilor,

deoarece $AC$ este partea lor comună și $AB=CD$ după condiție. Mijloace

\[\angle DAC=\angle ACB\]

Luați în considerare dreptele $AD$ și $CB$ și secantele lor $AC$ prin ultima egalitate între unghiurile situate obținem că $AD||CB$.) În consecință, prin definiție $1$, acest patrulater este un paralelogram;

Teorema a fost demonstrată.

Teorema 2

Dacă laturile opuse ale unui patrulater sunt egale între ele, atunci acesta este un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. În care $AD=BC$ și $AB=CD$. Să desenăm în ea o diagonală $AC$ (Fig. 3).

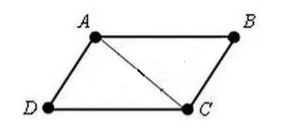
Figura 3.

Deoarece $AD=BC$, $AB=CD$ și $AC$ este o latură comună, atunci după criteriul $III$ pentru egalitatea triunghiurilor,

\[\triunghi DAC=\triunghi ACB\]

\[\angle DAC=\angle ACB\]

Să luăm în considerare liniile $AD$ și $CB$ și secantele lor $AC$ prin ultima egalitate peste unghiurile situate obținem acel $AD||CB$; Prin urmare, prin definiție $1$, acest patrulater este un paralelogram.

\[\angle DCA=\angle CAB\]

Să considerăm dreptele $AB$ și $CD$ și secantele lor $AC$ prin ultima egalitate peste unghiurile situate obținem acel $AB||CD$; Prin urmare, după Definiția 1, acest patrulater este un paralelogram.

Teorema a fost demonstrată.

Teorema 3

Dacă diagonalele desenate într-un patrulater sunt împărțite în două părți egale prin punctul lor de intersecție, atunci acest patrulater este un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. Să desenăm diagonalele $AC$ și $BD$ în el. Lasă-le să se intersecteze în punctul $O$ (Fig. 4).

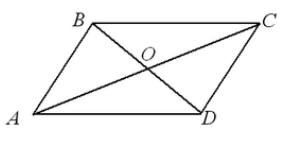
Figura 4.

Deoarece, prin condiție, $BO=OD,\ AO=OC$, iar unghiurile $\angle COB=\angle DOA$ sunt verticale, atunci, după criteriul $I$ pentru egalitatea triunghiurilor,

\[\triangle BOC=\triunghi AOD\]

\[\angle DBC=\angle BDA\]

Considerăm dreptele $BC$ și $AD$ și secantele lor $BD$ prin ultima egalitate peste unghiurile situate, obținem acel $BC||AD$; De asemenea, $BC=AD$. Prin urmare, după teorema $1$, acest patrulater este un paralelogram.