Care este varianța unei variabile aleatoare. Varianta reziduala

Tipuri de dispersii:

Varianta totala caracterizează variaţia unei caracteristici a întregii populaţii sub influenţa tuturor acelor factori care au determinat această variaţie. Această valoare este determinată de formulă

unde este media aritmetică globală a întregii populații studiate.

Varianta medie în cadrul grupului indică o variație aleatorie care poate apărea sub influența oricăror factori necontabilizați și care nu depinde de atributul-factor care formează baza grupării. Această variație se calculează după cum urmează: mai întâi, se calculează variațiile pentru grupuri individuale (), apoi se calculează variația medie în cadrul grupului:

unde n i este numărul de unități din grup

Varianta intergrup(varianta mijloacelor grupului) caracterizeaza variatia sistematica, i.e. diferențe de valoare a caracteristicii studiate care apar sub influența factorului-semn, care stă la baza grupării.

unde este valoarea medie pentru un grup separat.

Toate cele trei tipuri de varianță sunt legate între ele: varianța totală este egală cu suma variației medii în interiorul grupului și a variației între grupuri:

Proprietăți:

25 Măsuri relative ale variației

Coeficient de oscilație
Deviația liniară relativă
Coeficientul de variație

Coef. Osc. O reflectă fluctuația relativă a valorilor extreme ale unei caracteristici în jurul mediei. rel. lin. oprit. caracterizează proporţia valorii medii a semnului abaterilor absolute de la valoarea medie. Coef. Variația este cea mai comună măsură a variabilității utilizată pentru a evalua caracterul tipic al mediilor.

În statistică, populațiile cu un coeficient de variație mai mare de 30–35% sunt considerate eterogene.

Regularitatea serii de distribuție. Momente de distribuție.

Indicatori de formă de distribuție În seria de variații există o legătură între frecvențe și valorile caracteristicii variabile: cu o creștere a caracteristicii, valoarea frecvenței crește mai întâi până la o anumită limită și apoi scade. Se numesc astfel de schimbări

modele de distribuție.

Forma distribuției este studiată folosind indicatori de asimetrie și curtoză. La calcularea acestor indicatori se folosesc momentele de distribuție.

Momentul de ordinul k-lea este media gradelor k-lea de abatere a valorilor variante ale unei caracteristici de la o valoare constantă. Ordinea momentului este determinată de valoarea lui k. Când se analizează serii de variații, se limitează la calcularea momentelor primelor patru ordine. La calcularea momentelor, frecvențele sau frecvențele pot fi folosite ca ponderi. În funcție de alegerea valorii constante, se disting momentele inițiale, condiționale și centrale.

Indicatori de formă de distribuție: Asimetrie .

(As) indicator care caracterizează gradul de asimetrie a distribuției Prin urmare, cu asimetrie negativă (pe partea stângă). .

. Cu asimetrie pozitivă (pe partea dreaptă).

,

Momentele centrale pot fi folosite pentru a calcula asimetria. Apoi: 3 unde μ

- – momentul central de ordinul trei. curtoza (E ) La

,

caracterizează abruptul graficului funcției în comparație cu distribuția normală la aceeași putere de variație:

unde μ 4 este momentul central de ordinul al 4-lea.

Legea distribuției normale

Pentru o distribuție normală (distribuție Gauss), funcția de distribuție are următoarea formă:

Aşteptare - abatere standard

Distribuția normală este simetrică și se caracterizează prin următoarea relație: Xav=Me=Mo

Curtoza unei distribuții normale este 3, iar coeficientul de asimetrie este 0.

Curba de distribuție normală este un poligon (linie dreaptă simetrică în formă de clopot)

Tipuri de dispersii. Regula pentru adăugarea variațiilor.

Esența coeficientului empiric de determinare.

Dacă populația inițială este împărțită în grupuri în funcție de o caracteristică semnificativă, atunci se calculează următoarele tipuri de variații:

Varianța totală a populației inițiale:

unde j este numărul grupului este valoarea medie a fiecărei j-a grupă; Variantele intragrup caracterizează abaterea valorii individuale a unei trăsături din fiecare grup de la valoarea medie a grupului. Din toate variațiile în interiorul grupului, media este calculată folosind formula:, unde este numărul de unități din fiecare j-a grupă.

Varianta intergrup:

Dispersia intergrupurilor caracterizează abaterea mediilor grupului de la media generală a populației inițiale.

Regula de adunare a variațiilor este că varianța totală a populației inițiale ar trebui să fie egală cu suma dintre grup și medie a variațiilor în interiorul grupului:

Coeficientul empiric de determinare arată proporția de variație a caracteristicii studiate datorită variației caracteristicii de grupare și se calculează folosind formula:

Metoda de numărare de la zero condiționat (metoda momentelor) pentru calcularea valorii medii și a varianței

Calculul dispersiei prin metoda momentelor se bazează pe utilizarea formulei și a proprietăților 3 și 4 ale dispersiei.

(3. Dacă toate valorile atributului (opțiunilor) sunt mărite (scăzute) cu un număr constant A, atunci varianța noii populații nu se va modifica.

4. Dacă toate valorile atributului (opțiunilor) sunt mărite (înmulțite) cu K ori, unde K este un număr constant, atunci varianța noii populații va crește (scădea) cu K de 2 ori.)

Obținem o formulă pentru calcularea dispersiei în serii de variații cu intervale egale folosind metoda momentelor:

A - zero condiționat, egal cu opțiunea cu frecvența maximă (mijlocul intervalului cu frecvența maximă)

Calculul valorii medii prin metoda momentelor se bazează și pe utilizarea proprietăților mediei.

Conceptul de observație selectivă. Etapele studierii fenomenelor economice prin metoda de eșantionare

O observație prin eșantion este o observație în care nu sunt examinate și studiate toate unitățile populației inițiale, ci doar o parte a unităților, în timp ce rezultatul examinării unei părți a populației se aplică întregii populații inițiale. Se numește populația din care sunt selectate unitățile pentru examinare și studiu ulterioare general iar toţi indicatorii care caracterizează această totalitate se numesc general.

Sunt numite limitele posibile ale abaterilor valorii medii eșantionului față de valoarea medie generală eroare de eșantionare.

Setul de unități selectate este numit selectiv iar toţi indicatorii care caracterizează această totalitate se numesc selectiv.

Cercetarea eșantionului include următoarele etape:

Caracteristicile obiectului de studiu (fenomene economice de masă). Dacă populația este mică, nu este recomandată eșantionarea;

Calculul dimensiunii eșantionului. Este important să se determine volumul optim care va permite erorii de eșantionare să fie în intervalul acceptabil la cel mai mic cost;

Selectarea unităților de observare ținând cont de cerințele de aleatorie și proporționalitate.

Dovezi de reprezentativitate bazate pe o estimare a erorii de eșantionare. Pentru un eșantion aleatoriu, eroarea este calculată folosind formule. Pentru eșantionul țintă, reprezentativitatea este evaluată prin metode calitative (comparație, experiment);

Analiza populației eșantionului. Dacă eșantionul generat îndeplinește cerințele de reprezentativitate, atunci acesta este analizat folosind indicatori analitici (medii, relative etc.)

Pentru date grupate varianta reziduala- media variațiilor intragrup:

Unde σ 2 j este varianța intragrup a grupului j.

Pentru date negrupate varianta reziduala– măsura acurateței aproximării, adică aproximarea dreptei de regresie la datele originale:
unde y(t) este prognoza folosind ecuația tendinței; y t – serie de dinamică inițială; n – numărul de puncte; p – numărul de coeficienți ai ecuației de regresie (număr de variabile explicative).
În acest exemplu se numește estimator de varianță imparțial.

Exemplul nr. 1. Repartizarea lucrătorilor a trei întreprinderi ale unei asociații pe categorii tarifare se caracterizează prin următoarele date:

Categoria tarifară a lucrătorului	Numărul de lucrători la întreprindere
	intreprindere 1	intreprindere 2	intreprindere 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Defini:
1. varianță pentru fiecare întreprindere (varianțe intra-grup);
2. media variațiilor în interiorul grupului;
3. dispersie intergrup;
4. varianţa totală.

Soluţie.
Înainte de a începe să rezolvați problema, este necesar să aflați care caracteristică este eficientă și care este factorială. În exemplul luat în considerare, atributul rezultat este „Categoria tarifară”, iar atributul factor este „Numărul (numele) întreprinderii”.
Apoi avem trei grupuri (întreprinderi), pentru care este necesar să se calculeze media grupului și variațiile intragrup:

Întreprindere	Media grupului,	Varianta în cadrul grupului,
1	4	1,8

Media variațiilor în interiorul grupului ( varianta reziduala) se va calcula folosind formula:

unde poti calcula:
sau:

Apoi:
Varianta totala va fi egala cu: s 2 = 1,6 + 0 = 1,6.
De asemenea, variația totală poate fi calculată folosind una dintre următoarele două formule:

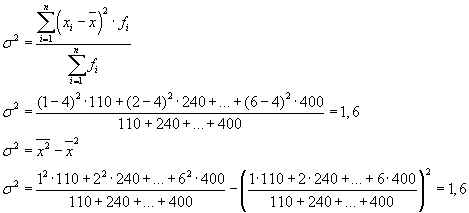
Când rezolvăm probleme practice, de multe ori trebuie să te confrunți cu o caracteristică care ia doar două valori alternative. În acest caz, nu vorbim despre ponderea unei anumite valori a unei caracteristici, ci despre ponderea acesteia în totalitate. Dacă proporția unităților de populație care posedă caracteristica studiată se notează cu „ r", iar cei care nu au - prin " q", atunci varianța poate fi calculată folosind formula:
s 2 = p×q

Exemplul nr. 2. Pe baza datelor de producție a șase lucrători dintr-o echipă, determinați varianța intergrup și evaluați impactul schimbului de muncă asupra productivității muncii lor dacă varianța totală este de 12,2.

Lucrator in echipa nr.	Ieșire muncitor, buc.
	în primul schimb	în al doilea schimb
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Soluţie. Datele inițiale

X	f 1	f 2	f 3	f 4	f 5	f 6	Total
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Total	31	33	37	37	40	38

Apoi avem 6 grupuri pentru care este necesar să se calculeze media grupului și variațiile intragrup.
1. Găsiți valorile medii ale fiecărui grup.







2. Aflați pătratul mediu al fiecărui grup.







Să rezumăm rezultatele calculului într-un tabel:

Numărul grupului	Media grupului	Varianta în cadrul grupului
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Varianta în cadrul grupului caracterizează schimbarea (variația) caracteristicii studiate (rezultate) în cadrul unui grup sub influența tuturor factorilor asupra acestuia, cu excepția factorului care stă la baza grupării:
Calculăm media variațiilor intragrup folosind formula:


4. Varianta intergrup caracterizează modificarea (variaţia) caracteristicii (rezultative) studiate sub influenţa unui factor (caracteristică factorială) care formează baza grupului.
Definim varianța intergrup ca fiind:

Unde


Apoi

Varianta totala caracterizează schimbarea (variația) caracteristicii (rezultate) studiate sub influența tuturor factorilor (caracteristicile factoriale) fără excepție. În funcție de condițiile problemei, este egal cu 12,2.
Relație de corelație empirică măsoară ce parte din variabilitatea totală a caracteristicii rezultate este cauzată de factorul studiat. Acesta este raportul dintre variația factorului la varianta totala:

Definim relația de corelație empirică:

Conexiunile dintre caracteristici pot fi slabe și puternice (strânse). Criteriile lor sunt evaluate pe scara Chaddock:
0,1 0,3 0,5 0,7 0,9 În exemplul nostru, relația dintre trăsătura Y și factorul X este slabă
Coeficient de determinare.

Să determinăm coeficientul de determinare:

Astfel, 0,67% din variație se datorează diferențelor dintre trăsături, iar 99,37% se datorează altor factori.
Concluzie: V în acest caz, Rezultatul lucrătorilor nu depinde de munca pe o anumită tură, de exemplu. influenţa schimbului de muncă asupra productivităţii muncii lor nu este semnificativă şi se datorează altor factori.

Exemplul nr. 3. Bazat pe medie salariile iar abaterile pătrate de la valoarea sa pentru două grupuri de lucrători, găsiți varianța totală prin aplicarea regulii de adunare a variațiilor:

Soluţie:
Media variațiilor în cadrul grupului

Definim varianța intergrup ca fiind:


Varianta totală va fi: 480 + 13824 = 14304

Pe lângă studierea variației unei caracteristici în întreaga populație în ansamblu, este adesea necesară urmărirea modificărilor cantitative ale caracteristicii în grupurile în care este împărțită populația, precum și între grupuri. Acest studiu al variației se realizează prin calcul și analiză diverse tipuri variaţiile.
Există variații totale, intergrup și intragrup.
Varianta totala σ 2 măsoară variația unei trăsături în întreaga populație sub influența tuturor factorilor care au determinat această variație.

Varianta intergrup (δ) caracterizează variația sistematică, adică. diferenţe de valoare a trăsăturii studiate care apar sub influenţa trăsăturii factoriale care formează baza grupului. Se calculează folosind formula:
.

Varianta în cadrul grupului (σ) reflectă variație aleatorie, adică parte a variației care apare sub influența factorilor necontabiliați și nu depinde de atributul-factorial care formează baza grupului. Se calculează prin formula:
.

Media variațiilor în cadrul grupului: .

Există o lege care leagă 3 tipuri de dispersie. Varianța totală este egală cu suma mediei variației în interiorul grupului și între grupuri: .
Acest raport se numește regula pentru adăugarea variațiilor.

Un indicator utilizat pe scară largă în analiză este proporția varianței între grupuri în varianța totală. Se numește coeficient empiric de determinare (η 2): .
Se numește rădăcina pătrată a coeficientului empiric de determinare raportul de corelație empirică (η):
.
Caracterizează influența caracteristicii care formează baza grupului asupra variației caracteristicii rezultate. Raportul de corelație empirică variază de la 0 la 1.
Să demonstrăm utilizarea sa practică folosind următorul exemplu (Tabelul 1).

Exemplul nr. 1. Tabelul 1 - Productivitatea muncii a două grupuri de lucrători într-unul din atelierele ONG „Ciclon”

Să calculăm mediile și variațiile globale și de grup:

Datele inițiale pentru calcularea mediei varianței intragrup și intergrup sunt prezentate în tabel. 2.
Tabelul 2
Calcul și δ 2 pentru două grupuri de lucrători.

Grupuri de muncitori	Număr de muncitori, oameni	Mediu, copii/schimb	Dispersia
Pregătire tehnică finalizată	5	95	42,0
Cei care nu au absolvit pregătirea tehnică	5	81	231,2
Toți muncitorii	10	88	185,6

Să calculăm indicatorii. Media variațiilor în cadrul grupului:
.
Varianta intergrup

Varianta totala:
Astfel, raportul de corelație empirică: .

Odată cu variația caracteristicilor cantitative, pot fi observate și variații în caracteristicile calitative. Acest studiu al variației se realizează prin calcularea următoarelor tipuri de variații:

Dispersia în interiorul grupului a cotei este determinată de formulă

Unde n i– numărul de unități în grupuri separate.
Ponderea caracteristicii studiate în întreaga populație, care este determinată de formula:
Cele trei tipuri de varianță sunt legate între ele, după cum urmează:
.

Această relație de varianțe se numește teorema de adunare a varianțelor cotei de trăsătură.

Dispersia variabilă aleatoare este o măsură a răspândirii valorilor acestei cantități. Varianta scăzută înseamnă că valorile sunt grupate strâns. Dispersia mare indică o răspândire puternică a valorilor. Conceptul de varianță a unei variabile aleatoare este utilizat în statistică. De exemplu, dacă comparați varianța a două valori (cum ar fi între pacienții de sex masculin și de sex feminin), puteți testa semnificația unei variabile. Varianta este, de asemenea, utilizată la construirea modelelor statistice, deoarece variația scăzută poate fi un semn că supraajustați valorile.

Pași

Calcularea varianței eșantionului

1. Înregistrați valorile eșantionului.În cele mai multe cazuri, statisticienii au acces doar la mostre de populații specifice. De exemplu, de regulă, statisticienii nu analizează costul întreținerii totalității tuturor mașinilor din Rusia - ei analizează un eșantion aleatoriu de câteva mii de mașini. Un astfel de eșantion va ajuta la determinarea costului mediu al unei mașini, dar, cel mai probabil, valoarea rezultată va fi departe de cea reală.

   • De exemplu, să analizăm numărul de chifle vândute într-o cafenea pe parcursul a 6 zile, luate în ordine aleatorie. Eșantionul arată astfel: 17, 15, 23, 7, 9, 13. Acesta este un eșantion, nu o populație, deoarece nu avem date despre chiflele vândute pentru fiecare zi în care cafeneaua este deschisă.
   • Dacă vi se oferă o populație mai degrabă decât un eșantion de valori, continuați la secțiunea următoare.

2. Scrieți o formulă pentru a calcula varianța eșantionului. Dispersia este o măsură a răspândirii valorilor unei anumite cantități. Cu cât valoarea varianței este mai aproape de zero, cu atât valorile sunt grupate mai aproape. Când lucrați cu un eșantion de valori, utilizați următoarea formulă pentru a calcula varianța:

   • s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))] / (n - 1)
   • s 2 (\displaystyle s^(2))– aceasta este dispersia. Dispersia se măsoară în unități pătrate.
   • x i (\displaystyle x_(i))– fiecare valoare din eșantion.
   • x i (\displaystyle x_(i)) trebuie să scădeți x̅, să-l pătrați și apoi să adăugați rezultatele.
   • x̅ – medie eșantion (medie eșantion).
   • n – numărul de valori din eșantion.

3. Calculați media eșantionului. Este notat cu x̅. Media eșantionului este calculată ca medie aritmetică simplă: se adună toate valorile din eșantion, apoi se împarte rezultatul la numărul de valori din eșantion.

   • În exemplul nostru, adăugați valorile din eșantion: 15 + 17 + 23 + 7 + 9 + 13 = 84
     Acum împărțiți rezultatul la numărul de valori din eșantion (în exemplul nostru sunt 6): 84 ÷ 6 = 14.
     Media eșantionului x̅ = 14.
   • Media eșantionului este valoarea centrală în jurul căreia sunt distribuite valorile din eșantion. Dacă valorile din grupul de eșantion din jurul eșantionului sunt medii, atunci varianța este mică; în caz contrar, varianța este mare.

4. Scădeți media eșantionului din fiecare valoare din eșantion. Acum calculează diferența x i (\displaystyle x_(i))- x̅, unde x i (\displaystyle x_(i))– fiecare valoare din eșantion. Fiecare rezultat obținut indică măsura în care o anumită valoare se abate de la media eșantionului, adică cât de departe este această valoare de media eșantionului.

   • În exemplul nostru:
     x 1 (\displaystyle x_(1))- x = 17 - 14 = 3
     x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
     x 3 (\displaystyle x_(3))- x = 23 - 14 = 9
     x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
     x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
     x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
   • Corectitudinea rezultatelor obținute este ușor de verificat, deoarece suma lor ar trebui să fie egală cu zero. Acest lucru este legat de determinarea valorii medii, deoarece valorile negative (distanțele de la valoarea medie la valori mai mici) sunt complet compensate valori pozitive(distanțele de la valori medii la mari).

5. După cum sa menționat mai sus, suma diferențelor x i (\displaystyle x_(i))- x̅ trebuie să fie egal cu zero. Aceasta înseamnă că varianța medie este întotdeauna zero, ceea ce nu dă nicio idee despre răspândirea valorilor unei anumite cantități. Pentru a rezolva această problemă, pătrați fiecare diferență x i (\displaystyle x_(i))- x̅. Acest lucru va avea ca rezultat doar obținerea numere pozitive, care atunci când este adăugată nu va da niciodată 0.

   • În exemplul nostru:
     (x 1 (\displaystyle x_(1))- x̅) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
     (x 2 (\displaystyle (x_(2)))- x̅) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
     9 2 = 81
     (-7) 2 = 49
     (-5) 2 = 25
     (-1) 2 = 1
   • Ai găsit pătratul diferenței - x̅) 2 (\displaystyle ^(2)) pentru fiecare valoare din eșantion.

6. Calculați suma pătratelor diferențelor. Adică, găsiți acea parte a formulei care este scrisă astfel: ∑[( x i (\displaystyle x_(i))- x̅) 2 (\displaystyle ^(2))]. Aici semnul Σ înseamnă suma diferențelor pătrate pentru fiecare valoare x i (\displaystyle x_(i))în probă. Ați găsit deja diferențele la pătrat (x i (\displaystyle (x_(i)))- x̅) 2 (\displaystyle ^(2)) pentru fiecare valoare x i (\displaystyle x_(i))în probă; acum doar adăugați aceste pătrate.

   • În exemplul nostru: 9 + 1 + 81 + 49 + 25 + 1 = 166 .

7. Împărțiți rezultatul la n - 1, unde n este numărul de valori din eșantion. Cu ceva timp în urmă, pentru a calcula varianța eșantionului, statisticienii au împărțit pur și simplu rezultatul la n; în acest caz, veți obține media varianței pătrate, care este ideală pentru a descrie varianța unui eșantion dat. Dar amintiți-vă că orice eșantion este doar o mică parte din populația de valori. Dacă luați o altă probă și efectuați aceleași calcule, veți obține un rezultat diferit. După cum se dovedește, împărțirea la n - 1 (mai degrabă decât doar n) oferă o estimare mai precisă a varianței populației, care este ceea ce vă interesează. Împărțirea cu n – 1 a devenit obișnuită, deci este inclusă în formula pentru calcularea varianței eșantionului.

   • În exemplul nostru, eșantionul include 6 valori, adică n = 6.
     Varianta eșantionului = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2

8. Diferența dintre varianță și abaterea standard. Rețineți că formula conține un exponent, astfel încât dispersia este măsurată în unități pătrate ale valorii analizate. Uneori, o astfel de mărime este destul de dificil de operat; în astfel de cazuri, utilizați abaterea standard, care este egală cu rădăcina pătrată a varianței. De aceea, varianța eșantionului se notează ca s 2 (\displaystyle s^(2)), iar abaterea standard a probei este ca s (\displaystyle s).

   • În exemplul nostru, abaterea standard a eșantionului este: s = √33,2 = 5,76.

   Calcularea variației populației

   1. Analizați un set de valori. Setul include toate valorile cantității luate în considerare. De exemplu, dacă studiezi vârsta rezidenților Regiunea Leningrad, atunci populația include vârstele tuturor locuitorilor acestei zone. Când lucrați cu o populație, se recomandă să creați un tabel și să introduceți valorile populației în el. Luați în considerare următorul exemplu:

      • Într-o anumită cameră sunt 6 acvarii. Fiecare acvariu conține următorul număr de pești:
        x 1 = 5 (\displaystyle x_(1)=5)
        x 2 = 5 (\displaystyle x_(2)=5)
        x 3 = 8 (\displaystyle x_(3)=8)
        x 4 = 12 (\displaystyle x_(4)=12)
        x 5 = 15 (\displaystyle x_(5)=15)
        x 6 = 18 (\displaystyle x_(6)=18)

   2. Scrieți o formulă pentru a calcula varianța populației.Întrucât totalitatea include toate valorile unei anumite cantități, formula de mai jos ne permite să obținem valoarea exacta variaţiile populaţiei. Pentru a distinge varianța populației de varianța eșantionului (care este doar o estimare), statisticienii folosesc diverse variabile:

      • σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)))/n
      • σ 2 (\displaystyle ^(2))– dispersia populației (a se citi „sigma pătrat”). Dispersia se măsoară în unități pătrate.
      • x i (\displaystyle x_(i))– fiecare valoare în total.
      • Σ – semnul sumei. Adică din fiecare valoare x i (\displaystyle x_(i)) trebuie să scădeți μ, să-l pătrați și apoi să adăugați rezultatele.
      • μ – media populației.
      • n – numărul de valori din populație.

   3. Calculați media populației. Când se lucrează cu o populație, media ei este notată ca μ (mu). Media populației este calculată ca medie aritmetică simplă: se adună toate valorile din populație și apoi se împarte rezultatul la numărul de valori din populație.

      • Rețineți că mediile nu sunt întotdeauna calculate ca medie aritmetică.
      • În exemplul nostru, media populației: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5

   4. Scădeți media populației din fiecare valoare din populație. Cu cât diferența este mai aproape de zero, cu atât valoarea specifică este mai aproape de media populației. Găsiți diferența dintre fiecare valoare din populație și media acesteia și vă veți face o primă idee despre distribuția valorilor.

      • În exemplul nostru:
        x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
        x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
        x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
        x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
        x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
        x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5

   5. Patratează fiecare rezultat obținut. Valorile diferențelor vor fi atât pozitive, cât și negative; Dacă aceste valori sunt reprezentate pe o linie numerică, ele se vor afla la dreapta și la stânga mediei populației. Acest lucru nu este potrivit pentru calcularea varianței, deoarece pozitiv și numere negative compensa reciproc. Deci pătrați fiecare diferență pentru a obține numere exclusiv pozitive.

      • În exemplul nostru:
        (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2)) pentru fiecare valoare a populației (de la i = 1 la i = 6):
        (-5,5)2 (\displaystyle ^(2)) = 30,25
        (-5,5)2 (\displaystyle ^(2)), Unde x n (\displaystyle x_(n))– ultima valoare din populatie.
      • Pentru a calcula valoarea medie a rezultatelor obținute, trebuie să găsiți suma lor și să o împărțiți la n:(( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2)))/n
      • Acum să scriem explicația de mai sus folosind variabile: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n și obțineți o formulă pentru calcularea varianței populației.

Cu toate acestea, această caracteristică singură nu este suficientă pentru a studia o variabilă aleatorie. Să ne imaginăm doi trăgători trăgând la o țintă. Unul trage cu precizie și lovește aproape de centru, în timp ce celălalt... se distrează și nici măcar nu țintește. Dar ce e amuzant este că el medie rezultatul va fi exact același cu primul shooter! Această situație este ilustrată în mod convențional de următoarele variabile aleatoare:

Așteptarea matematică „lunetist” este egală cu , însă, pentru „persoana interesantă”: – este și zero!

Astfel, este necesar să se cuantifice cât de departe risipite gloanțe (valori ale variabilelor aleatoare) raportate la centrul țintei (așteptări matematice). Bine împrăștiere tradus din latină nu este altfel decât dispersie .

Să vedem cum se determină acest lucru caracteristica numerica folosind unul dintre exemplele din prima parte a lecției:

Acolo am găsit o așteptare matematică dezamăgitoare a acestui joc, iar acum trebuie să calculăm varianța acestuia, care notat cu prin .

Să aflăm cât de mult sunt „împrăștiate” câștigurile/pierderile față de valoarea medie. Evident, pentru asta trebuie să calculăm diferențeîntre valori ale variabilelor aleatoare si ea așteptări matematice:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Acum se pare că trebuie să rezumați rezultatele, dar această cale nu este potrivită - din motivul că fluctuațiile din stânga se vor anula reciproc cu fluctuații spre dreapta. Deci, de exemplu, un trăgător „amator”. (exemplu de mai sus) diferențele vor fi , iar atunci când sunt adăugate vor da zero, așa că nu vom obține nicio estimare a dispersiei împușcării sale.

Pentru a ocoli această problemă, puteți lua în considerare module diferențe, dar din motive tehnice abordarea a prins rădăcini atunci când sunt pătrate. Este mai convenabil să formulați soluția într-un tabel:

Și aici se cere să calculeze medie ponderată valoarea abaterilor pătrate. Și CE este asta? Este al lor așteptări matematice, care este o măsură a împrăștierii:

– definiţie variaţiile. Din definiție reiese imediat că varianța nu poate fi negativă– ia notă pentru practică!

Să ne amintim cum să găsim valoarea așteptată. Înmulțiți diferențele la pătrat cu probabilitățile corespunzătoare (continuare tabel):
– la sens figurat, aceasta este „forța de tracțiune”,
și rezumă rezultatele:

Nu crezi că, în comparație cu câștigurile, rezultatul s-a dovedit a fi prea mare? Așa este - l-am pătrat și pentru a reveni la dimensiunea jocului nostru, trebuie să extragem rădăcină pătrată. Această cantitate se numește abaterea standard și este notat cu litera greacă „sigma”:

Această valoare este uneori numită abaterea standard .

Care este sensul lui? Dacă ne abatem de la așteptarea matematică la stânga și la dreapta cu medie abaterea standard:

– atunci cele mai probabile valori ale variabilei aleatoare vor fi „concentrate” pe acest interval. Ce observăm de fapt:

Cu toate acestea, se întâmplă că atunci când se analizează împrăștierea se operează aproape întotdeauna cu conceptul de dispersie. Să ne dăm seama ce înseamnă în legătură cu jocuri. Dacă în cazul săgeților vorbim despre „precizia” lovirilor în raport cu centrul țintei, atunci dispersia caracterizează două lucruri:

În primul rând, este evident că pe măsură ce pariurile cresc, și dispersia crește. Deci, de exemplu, dacă creștem de 10 ori, atunci așteptarea matematică va crește de 10 ori, iar varianța va crește de 100 de ori (deoarece aceasta este o cantitate pătratică). Dar rețineți că regulile jocului în sine nu s-au schimbat! Doar ratele s-au schimbat, aproximativ vorbind, înainte de a paria 10 ruble, acum sunt 100.

Al doilea punct, mai interesant, este că variația caracterizează stilul de joc. Fixați mental pariurile jocului la un anumit nivel, și să vedem ce este:

Un joc cu variație scăzută este un joc precaut. Jucătorul tinde să aleagă cele mai fiabile scheme, unde nu pierde/câștigă prea mult la un moment dat. De exemplu, sistemul roșu/negru la ruletă (vezi exemplul 4 al articolului Variabile aleatorii) .

Joc cu variație mare. Ea este numită des dispersiv joc. Acesta este un stil de joc aventuros sau agresiv, în care jucătorul alege scheme de „adrenalină”. Să ne amintim măcar "Martingala", în care sumele puse în joc sunt ordine de mărime mai mari decât jocul „liniștit” de la punctul precedent.

Situația în poker este orientativă: există așa-zise strâns jucători care au tendința de a fi precauți și „tremurați” cu privire la fondurile lor de jocuri (bankroll). Nu este surprinzător, bankroll-ul lor nu fluctuează semnificativ (varianță scăzută). Dimpotrivă, dacă un jucător are o variație mare, atunci el este un agresor. Adesea își asumă riscuri, face pariuri mari și poate fie să spargă o bancă uriașă, fie să se piardă în bucăți.

Același lucru se întâmplă în Forex și așa mai departe - există o mulțime de exemple.

Mai mult, în toate cazurile nu contează dacă jocul este jucat pentru bani sau mii de dolari. Fiecare nivel are jucătorii săi cu dispersie scăzută și mare. Ei bine, după cum ne amintim, câștigul mediu este „responsabil” așteptări matematice.

Probabil ați observat că găsirea variației este un proces lung și minuțios. Dar matematica este generoasă:

Formula pentru găsirea varianței

Această formulă este derivată direct din definiția varianței și o punem imediat în uz. Voi copia semnul cu jocul nostru de mai sus:

și așteptarea matematică găsită.

Să calculăm varianța în al doilea mod. Mai întâi, să găsim așteptarea matematică - pătratul variabilei aleatoare. De determinarea așteptărilor matematice:

În acest caz:

Astfel, conform formulei:

După cum se spune, simți diferența. Și în practică, desigur, este mai bine să utilizați formula (cu excepția cazului în care condiția cere altfel).

Stăpânim tehnica de rezolvare și proiectare:

Exemplul 6

Găsiți așteptările sale matematice, varianța și abaterea standard.

Această sarcină se găsește peste tot și, de regulă, nu are sens semnificativ.
Vă puteți imagina mai multe becuri cu cifre care se aprind într-un cămin de nebuni cu anumite probabilități :)

Soluţie: Este convenabil să rezumați calculele de bază într-un tabel. Mai întâi, scriem datele inițiale în primele două rânduri. Apoi calculăm produsele, apoi și în final sumele din coloana din dreapta:

De fapt, aproape totul este gata. A treia linie arată o așteptare matematică gata făcută: .

Să calculăm varianța folosind formula:

Și în sfârșit, abaterea standard:
– Personal, de obicei rotunjesc la 2 zecimale.

Toate calculele pot fi efectuate pe un calculator sau chiar mai bine - în Excel:

E greu să greșești aici :)

Răspuns:

Cei care doresc își pot simplifica și mai mult viața și pot profita de mine calculator (demo), care nu numai că va rezolva instantaneu această problemă, ci și va construi grafică tematică (o sa ajungem acolo in curand). Programul poate fi descărcați din bibliotecă– dacă ați descărcat cel puțin unul material educativ, sau obține alt mod. Vă mulțumim pentru susținerea proiectului!

Câteva sarcini pentru decizie independentă:

Exemplul 7

Calculați varianța variabilei aleatoare din exemplul anterior prin definiție.

Si un exemplu asemanator:

Exemplul 8

O variabilă aleatorie discretă este specificată de legea sa de distribuție:

Da, valorile variabilelor aleatoare pot fi destul de mari (exemplu din munca adevarata) , și aici, dacă este posibil, folosiți Excel. Așa cum, apropo, în Exemplul 7 - este mai rapid, mai fiabil și mai plăcut.

Soluții și răspunsuri în partea de jos a paginii.

Pentru a încheia partea a 2-a a lecției, ne vom uita la o altă problemă tipică, s-ar putea spune chiar un mic puzzle:

Exemplul 9

O variabilă aleatoare discretă poate lua doar două valori: și , și . Probabilitatea, așteptările matematice și varianța sunt cunoscute.

Soluţie: Să începem cu o probabilitate necunoscută. Deoarece o variabilă aleatorie poate lua doar două valori, suma probabilităților evenimentelor corespunzătoare este:

iar de atunci .

Rămâne doar să găsești..., e ușor de spus :) Dar ei bine, iată. Prin definiția așteptărilor matematice:
– înlocuirea cantităților cunoscute:

– și nimic mai mult nu poate fi stors din această ecuație, cu excepția faptului că o puteți rescrie în direcția obișnuită:

sau:

Cred că poți ghici următorii pași. Să compunem și să rezolvăm sistemul:

zecimale- aceasta, desigur, este o rușine totală; înmulțiți ambele ecuații cu 10:

si imparti la 2:

E mai bine. Din prima ecuație exprimăm:
(acesta este calea mai ușoară)– înlocuiți în a 2-a ecuație:

Construim pătratși faceți simplificări:

Înmulțiți cu:

Rezultatul a fost ecuație pătratică, găsim că este discriminant:
- Grozav!

și obținem două soluții:

1) dacă , Asta ;

2) dacă , Asta .

Prima pereche de valori satisface condiția. Cu o probabilitate mare, totul este corect, dar, cu toate acestea, să notăm legea distribuției:

și efectuați o verificare, și anume, găsiți așteptarea: