Em que proporção as alturas se cruzam? Elementos básicos do triângulo abc

E A → ⋅ B C → + E B → ⋅ C A → + E C → ⋅ A B → = 0 (\displaystyle (\overrightarrow (EA))\cdot (\overrightarrow (BC))+(\overrightarrow (EB))\cdot (\ overrightarrow (CA))+(\overrightarrow (EC))\cdot (\overrightarrow (AB))=0)

(Para provar a identidade, você deve usar as fórmulas

A B → = E B → − E A → , B C → = E C → − E B → , C A → = E A → − E C → (\displaystyle (\overrightarrow (AB))=(\overrightarrow (EB))-(\overrightarrow (EA) )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (CE)))

O ponto E deve ser considerado como a intersecção de duas alturas do triângulo.)

• Ortocentro isogonalmente conjugado ao centro circundar .
• Ortocentro está na mesma linha que o centróide, o centro circundar e o centro do círculo de nove pontos (ver linha reta de Euler).
• Ortocentro de um triângulo acutângulo é o centro do círculo inscrito em seu ortotriângulo.
• O centro de um triângulo descrito pelo ortocentro com vértices nos pontos médios dos lados do triângulo dado. O último triângulo é chamado de triângulo complementar ao primeiro triângulo.
• A última propriedade pode ser formulada da seguinte forma: O centro do círculo circunscrito ao triângulo serve ortocentro triângulo adicional.
• Pontos, simétricos ortocentro de um triângulo em relação aos seus lados estão na circunferência circunscrita.
• Pontos, simétricos ortocentro os triângulos relativos aos pontos médios dos lados também ficam no círculo circunscrito e coincidem com pontos diametralmente opostos aos vértices correspondentes.
• Se SOBREé o centro do círculo circunscrito ΔABC, então O H → = O A → + O B → + O C → (\displaystyle (\overrightarrow (OH))=(\overrightarrow (OA))+(\overrightarrow (OB))+(\overrightarrow (OC))) ,
• A distância do vértice do triângulo ao ortocentro é duas vezes maior que a distância do centro da circunferência circunscrita ao lado oposto.
• Qualquer segmento extraído de ortocentro antes da interseção com o círculo circunscrito, ele é sempre cortado ao meio pelo círculo de Euler. Ortocentroé o centro homotético desses dois círculos.
• Teorema de Hamilton. Três segmentos de linha conectando o ortocentro aos vértices do triângulo agudo dividem-no em três triângulos tendo o mesmo círculo de Euler (círculo de nove pontos) que o triângulo agudo original.
• Corolários do teorema de Hamilton:
  • Três segmentos de reta conectando o ortocentro aos vértices de um triângulo agudo dividem-no em três Triângulo de Hamilton tendo raios iguais de círculos circunscritos.
  • Os raios dos círculos circunscritos de três Triângulos de Hamilton igual ao raio do círculo circunscrito ao triângulo agudo original.
• Num triângulo acutângulo, o ortocentro está dentro do triângulo; em um ângulo obtuso - fora do triângulo; em retangular - no vértice de um ângulo reto.

Propriedades das altitudes de um triângulo isósceles

• Se duas altitudes em um triângulo são iguais, então o triângulo é isósceles (o teorema de Steiner-Lemus), e a terceira altitude é a mediana e a bissetriz do ângulo do qual emerge.
• O inverso também é verdadeiro: em um triângulo isósceles, duas altitudes são iguais e a terceira altitude é a mediana e a bissetriz.
• Um triângulo equilátero tem todas as três alturas iguais.

Propriedades das bases das alturas de um triângulo

• Terrenos as alturas formam um chamado ortotriângulo, que possui propriedades próprias.
• O círculo circunscrito a um ortotriângulo é o círculo de Euler. Este círculo também contém três pontos médios dos lados do triângulo e três pontos médios de três segmentos que conectam o ortocentro aos vértices do triângulo.
• Outra formulação da última propriedade:
  • Teorema de Euler para o círculo de nove pontos. Terrenos três alturas triângulo arbitrário, os pontos médios de seus três lados ( os fundamentos do seu interior medianas) e os pontos médios de três segmentos que conectam seus vértices ao ortocentro, todos ficam no mesmo círculo (em círculo de nove pontos).
• Teorema. Em qualquer triângulo, o segmento que liga motivos dois alturas triângulo, corta um triângulo semelhante ao dado.
• Teorema. Num triângulo, o segmento que liga motivos dois alturas triângulos deitados em dois lados antiparalelo a um terceiro com quem não tenha pontos em comum. Um círculo sempre pode ser traçado pelas suas duas extremidades, bem como pelos dois vértices do terceiro lado mencionado.

Outras propriedades das altitudes do triângulo

Propriedades da altitude mínima de um triângulo

A altitude mínima de um triângulo possui muitas propriedades extremas. Por exemplo:

• A projeção ortogonal mínima de um triângulo nas linhas situadas no plano do triângulo tem um comprimento igual à menor de suas altitudes.
• O corte reto mínimo em um plano através do qual uma placa triangular rígida pode ser tracionada deve ter comprimento igual à menor das alturas desta placa.
• Com o movimento contínuo de dois pontos ao longo do perímetro do triângulo em direção um ao outro, a distância máxima entre eles durante o movimento do primeiro encontro para o segundo não pode ser menor que o comprimento da menor altura do triângulo.
• A altura mínima em um triângulo sempre está dentro desse triângulo.

Relacionamentos básicos

• ha = b pecado ⁡ γ = c pecado ⁡ β , (\displaystyle h_(a)=b\sin \gamma =c\sin \beta ,)
• h a = 2 S a , (\displaystyle h_(a)=(\frac (2S)(a)),) Onde S (\estilo de exibição S)- área de um triângulo, uma (\estilo de exibição a)- o comprimento do lado do triângulo pelo qual a altura é reduzida.
• h a 2 = 1 2 (b 2 + c 2 − 1 2 (a 2 + (b 2 − c 2) 2 a 2)) (\displaystyle h_(a)^(2)=(\frac (1)(2 ))(b^(2)+c^(2)-(\frac (1)(2))(a^(2)+(\frac ((b^(2)-c^(2))^ (2))(uma^(2))))))
• h a = b c 2 R , (\displaystyle h_(a)=(\frac (bc)(2R)),) Onde b c (\estilo de exibição bc)- produto dos lados, R − (\estilo de exibição R-) raio do círculo circunscrito
• h a: h b: h c = 1 a: 1 b: 1 c = b c: a c: a b (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):( \frac (1)(b)):(\frac (1)(c))=bc:ac:ab)
• 1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (c)))=(\frac(1)(r))), Onde r (\estilo de exibição r)- raio do círculo inscrito.
• S = 1 (1 ha + 1 h b + 1 h c) ⋅ (1 ha + 1 h b - 1 h c) ⋅ (1 ha + 1 h c - 1 h b) ⋅ (1 h b + 1 h c - 1 h a) (\ displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a))))))))), Onde S (\estilo de exibição S)- área de um triângulo.
• a = 2 ha ⋅ (1 ha + 1 h b + 1 h c) ⋅ (1 ha + 1 h b - 1 h c) ⋅ (1 ha + 1 h c - 1 h b) ⋅ (1 h b + 1 h c - 1 h a) (\ estilo de exibição a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (a))))))))), uma (\estilo de exibição a)- o lado do triângulo para o qual a altura desce ha (\estilo de exibição h_(a)).
• Altura de um triângulo isósceles baixado até a base: h c = 1 2 4 a 2 − c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\sqrt (4a^(2)-c^(2))),)

Onde c (\estilo de exibição c)- base, uma (\estilo de exibição a)- lado.

Teorema da Altitude do Triângulo Retângulo

Se a altura em um triângulo retângulo A B C (\estilo de exibição ABC) comprimento h (\estilo de exibição h) desenhado a partir do vértice de um ângulo reto, divide a hipotenusa pelo comprimento c (\estilo de exibição c) em segmentos m (\estilo de exibição m) E n (\estilo de exibição n), correspondente às pernas b (\estilo de exibição b) E uma (\estilo de exibição a), então as seguintes igualdades são verdadeiras.

Triângulos.

Conceitos Básicos.

Triânguloé uma figura composta por três segmentos e três pontos que não estão na mesma linha reta.

Os segmentos são chamados festas, e os pontos são picos.

Soma dos ângulos triângulo é 180º.

Altura do triângulo.

Altura do triângulo- esta é uma perpendicular traçada do vértice ao lado oposto.

Em um triângulo agudo, a altura está contida dentro do triângulo (Fig. 1).

Em um triângulo retângulo, os catetos são as alturas do triângulo (Fig. 2).

Em um triângulo obtuso, a altitude se estende para fora do triângulo (Fig. 3).

Propriedades da altitude de um triângulo:

Bissetriz de um triângulo.

Bissetriz de um triângulo- este é um segmento que divide o canto do vértice ao meio e conecta o vértice a um ponto do lado oposto (Fig. 5).

Propriedades da bissetriz:

Mediana de um triângulo.

Mediana de um triângulo- este é um segmento que liga o vértice ao meio do lado oposto (Fig. 9a).

O comprimento da mediana pode ser calculado usando a fórmula: 2b 2 + 2c 2 - a 2 eu sou 2 = —————— 4 Onde eu sou- mediana desenhada para o lado A. Em um triângulo retângulo, a mediana traçada até a hipotenusa é igual à metade da hipotenusa: c m c = — 2 Onde m c- mediana desenhada para a hipotenusa c(Fig.9c) As medianas do triângulo se cruzam em um ponto (no centro de massa do triângulo) e são divididas por este ponto na proporção de 2:1, contando a partir do vértice. Ou seja, o segmento do vértice ao centro é duas vezes maior que o segmento do centro ao lado do triângulo (Fig. 9c). As três medianas de um triângulo o dividem em seis triângulos iguais.

A linha média do triângulo.

Linha média do triângulo- este é um segmento que conecta os pontos médios de seus dois lados (Fig. 10).

A linha média do triângulo é paralela ao terceiro lado e igual à metade dele

Ângulo externo de um triângulo.

Canto externo de um triângulo é igual à soma de dois ângulos internos não adjacentes (Fig. 11).

Um ângulo externo de um triângulo é maior que qualquer ângulo não adjacente.

Triângulo retângulo.

Triângulo retânguloé um triângulo que tem um ângulo reto (Fig. 12).

O lado de um triângulo retângulo oposto ao ângulo reto é chamado hipotenusa.

Os outros dois lados são chamados pernas.

Segmentos proporcionais em um triângulo retângulo.

1) Em um triângulo retângulo, a altitude traçada a partir do ângulo reto forma três triângulos semelhantes: ABC, ACH e HCB (Fig. 14a). Conseqüentemente, os ângulos formados pela altura são iguais aos ângulos A e B.

Figura 14a

Triângulo isósceles.

Triângulo isóscelesé um triângulo cujos dois lados são iguais (Fig. 13).

Esses lados iguais são chamados lados, e o terceiro - base triângulo.

Em um triângulo isósceles, os ângulos da base são iguais. (Em nosso triângulo, o ângulo A é igual ao ângulo C).

Em um triângulo isósceles, a mediana desenhada até a base é a bissetriz e a altura do triângulo.

Triângulo Equilátero.

Um triângulo equilátero é um triângulo em que todos os lados são iguais (Fig. 14).

Propriedades de um triângulo equilátero:

Propriedades notáveis ​​dos triângulos.

Os triângulos possuem propriedades únicas que o ajudarão a resolver problemas envolvendo essas formas com sucesso. Algumas dessas propriedades são descritas acima. Mas nós os repetimos novamente, adicionando alguns outros recursos maravilhosos:

1) Em um triângulo retângulo com ângulos de catetos de 90º, 30º e 60º b, oposto a um ângulo de 30º, é igual a metade da hipotenusa. Uma pernaa mais pernab√3 vezes (Fig. 15 A). Por exemplo, se a perna b for 5, então a hipotenusa c necessariamente é igual a 10, e a perna Aé igual a 5√3. 2) Em um triângulo isósceles retângulo com ângulos de 90º, 45º e 45º, a hipotenusa é √2 vezes maior que o cateto (Fig. 15). b). Por exemplo, se os catetos são 5, então a hipotenusa é 5√2. 3) A linha média do triângulo é igual à metade do lado paralelo (Fig. 15 Com). Por exemplo, se o lado de um triângulo é 10, então a linha média paralela a ele é 5. 4) Num triângulo retângulo, a mediana traçada até a hipotenusa é igual à metade da hipotenusa (Fig. 9c): m c= s/2. 5) As medianas de um triângulo, que se cruzam em um ponto, são divididas por este ponto na proporção de 2:1. Ou seja, o segmento do vértice ao ponto de intersecção das medianas é duas vezes maior que o segmento do ponto de intersecção das medianas ao lado do triângulo (Fig. 9c) 6) Em um triângulo retângulo, o meio da hipotenusa é o centro do círculo circunscrito (Fig. 15 d).

Sinais de igualdade de triângulos.

Primeiro sinal de igualdade: se dois lados e o ângulo entre eles de um triângulo são iguais a dois lados e o ângulo entre eles de outro triângulo, então tais triângulos são congruentes.

Segundo sinal de igualdade: se um lado e seus ângulos adjacentes de um triângulo são iguais ao lado e seus ângulos adjacentes de outro triângulo, então tais triângulos são congruentes.

Terceiro sinal de igualdade: Se três lados de um triângulo são iguais a três lados de outro triângulo, então esses triângulos são congruentes.

Desigualdade triangular.

Em qualquer triângulo, cada lado é menor que a soma dos outros dois lados.

Teorema de Pitágoras.

Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos:

c 2 = a 2 + b 2 .

Área de um triângulo.

1) A área de um triângulo é igual à metade do produto do seu lado pela altura desenhada para este lado:

ah
S = ——
2

2) A área de um triângulo é igual à metade do produto de quaisquer dois de seus lados pelo seno do ângulo entre eles:

1
S = — AB · A.C. · pecado A
2

Um triângulo circunscrito a um círculo.

Um círculo é chamado de inscrito em um triângulo se toca todos os seus lados (Fig. 16 A).

Um triângulo inscrito em um círculo.

Diz-se que um triângulo está inscrito em um círculo se o toca com todos os seus vértices (Fig. 17 a).

Seno, cosseno, tangente, cotangente de um ângulo agudo de um triângulo retângulo (Fig. 18).

Seioângulo agudo x oposto perna até a hipotenusa.
É denotado da seguinte forma: pecadox.

Cossenoângulo agudo x de um triângulo retângulo é a razão adjacente perna até a hipotenusa.
Denotado da seguinte forma: cos x.

Tangenteângulo agudo x- esta é a razão entre o lado oposto e o lado adjacente.
É designado da seguinte forma: tgx.

Co-tangenteângulo agudo x- esta é a razão entre o lado adjacente e o lado oposto.
É designado da seguinte forma: ctgx.

Regras:

Perna oposta ao canto x, é igual ao produto da hipotenusa e do pecado x:

b = c pecado x

Perna adjacente ao canto x, é igual ao produto da hipotenusa e cos x:

uma = c porque x

Perna oposta ao canto x, é igual ao produto da segunda etapa por tg x:

b = uma tg x

Perna adjacente ao canto x, é igual ao produto da segunda etapa por ctg x:

uma = b· ctg x.

Para qualquer ângulo agudo x:

pecado (90° - x) = porque x

cos (90° - x) = pecado x

Triângulo) ou passe fora do triângulo em um triângulo obtuso.

YouTube enciclopédico

1 / 5

✪ ALTURA MEDIANA BIssetriz de um triângulo Grau 7

✪ bissetriz, mediana, altitude de um triângulo. Geometria 7º ano

✪ 7ª série, lição 17, Medianas, bissetrizes e altitudes de um triângulo

✪ Mediana, bissetriz, altitude do triângulo | Geometria

✪ Como encontrar o comprimento da bissetriz, mediana e altura? | Nerd comigo #031 | Boris Trushin

Legendas

Propriedades do ponto de intersecção de três alturas de um triângulo (ortocentro)

E A → ⋅ B C → + E B → ⋅ C A → + E C → ⋅ A B → = 0 (\displaystyle (\overrightarrow (EA))\cdot (\overrightarrow (BC))+(\overrightarrow (EB))\cdot (\ overrightarrow (CA))+(\overrightarrow (EC))\cdot (\overrightarrow (AB))=0)

(Para provar a identidade, você deve usar as fórmulas

A B → = E B → − E A → , B C → = E C → − E B → , C A → = E A → − E C → (\displaystyle (\overrightarrow (AB))=(\overrightarrow (EB))-(\overrightarrow (EA) )),\,(\overrightarrow (BC))=(\overrightarrow (EC))-(\overrightarrow (EB)),\,(\overrightarrow (CA))=(\overrightarrow (EA))-(\overrightarrow (CE)))

O ponto E deve ser considerado como a intersecção de duas alturas do triângulo.)

• Ortocentro isogonalmente conjugado ao centro círculo circunscrito .
• Ortocentro está na mesma linha que o centróide, o centro circundar e o centro de um círculo de nove pontos (ver reta de Euler).
• Ortocentro de um triângulo acutângulo é o centro do círculo inscrito em seu ortotriângulo.
• O centro de um triângulo descrito pelo ortocentro com vértices nos pontos médios dos lados do triângulo dado. O último triângulo é chamado de triângulo complementar ao primeiro triângulo.
• A última propriedade pode ser formulada da seguinte forma: O centro do círculo circunscrito ao triângulo serve ortocentro triângulo adicional.
• Pontos, simétricos ortocentro de um triângulo em relação aos seus lados estão na circunferência circunscrita.
• Pontos, simétricos ortocentro os triângulos relativos aos pontos médios dos lados também ficam no círculo circunscrito e coincidem com pontos diametralmente opostos aos vértices correspondentes.
• Se O é o centro da circunferência circunscrita ΔABC, então O H → = O A → + O B → + O C → (\displaystyle (\overrightarrow (OH))=(\overrightarrow (OA))+(\overrightarrow (OB))+(\overrightarrow (OC))) ,
• A distância do vértice do triângulo ao ortocentro é duas vezes maior que a distância do centro da circunferência circunscrita ao lado oposto.
• Qualquer segmento extraído de ortocentro Antes de cruzar com o círculo circunscrito, ele é sempre dividido ao meio pelo círculo de Euler. Ortocentroé o centro homotético desses dois círculos.
• Teorema de Hamilton. Três segmentos de linha reta conectando o ortocentro aos vértices de um triângulo agudo dividem-no em três triângulos tendo o mesmo círculo de Euler (círculo de nove pontos) que o triângulo agudo original.
• Corolários do teorema de Hamilton:
  • Três segmentos de reta conectando o ortocentro aos vértices de um triângulo agudo dividem-no em três Triângulo de Hamilton tendo raios iguais de círculos circunscritos.
  • Os raios dos círculos circunscritos de três Triângulos de Hamilton igual ao raio do círculo circunscrito ao triângulo agudo original.
• Num triângulo acutângulo, o ortocentro está dentro do triângulo; em um ângulo obtuso - fora do triângulo; em retangular - no vértice de um ângulo reto.

Propriedades das altitudes de um triângulo isósceles

• Se duas altitudes em um triângulo são iguais, então o triângulo é isósceles (o teorema de Steiner-Lemus), e a terceira altitude é a mediana e a bissetriz do ângulo do qual emerge.
• O inverso também é verdadeiro: em um triângulo isósceles, duas altitudes são iguais e a terceira altitude é a mediana e a bissetriz.
• Um triângulo equilátero tem todas as três alturas iguais.

Propriedades das bases das alturas de um triângulo

• Terrenos as alturas formam um chamado ortotriângulo, que possui propriedades próprias.
• O círculo circunscrito a um ortotriângulo é o círculo de Euler. Este círculo também contém três pontos médios dos lados do triângulo e três pontos médios de três segmentos que conectam o ortocentro aos vértices do triângulo.
• Outra formulação da última propriedade:
  • Teorema de Euler para um círculo de nove pontos. Terrenos três alturas triângulo arbitrário, os pontos médios de seus três lados ( os fundamentos do seu interior medianas) e os pontos médios de três segmentos que conectam seus vértices ao ortocentro, todos ficam no mesmo círculo (em círculo de nove pontos).
• Teorema. Em qualquer triângulo, o segmento que liga motivos dois alturas triângulo, corta um triângulo semelhante ao dado.
• Teorema. Num triângulo, o segmento que liga motivos dois alturas triângulos deitados em dois lados antiparalelo a um terceiro com quem não tenha pontos em comum. Um círculo sempre pode ser traçado pelas suas duas extremidades, bem como pelos dois vértices do terceiro lado mencionado.

Outras propriedades das altitudes do triângulo

• Se um triângulo versátil (escaleno), então isso interno a bissetriz desenhada de qualquer vértice fica entre interno mediana e altura extraídas do mesmo vértice.
• A altura de um triângulo é isogonalmente conjugada ao diâmetro (raio) círculo circunscrito, extraído do mesmo vértice.
• Num triângulo acutângulo existem dois alturas corte triângulos semelhantes dele.
• Em um triângulo retângulo altura, desenhado a partir do vértice de um ângulo reto, divide-o em dois triângulos semelhantes ao original.

Propriedades da altitude mínima de um triângulo

A altitude mínima de um triângulo possui muitas propriedades extremas. Por exemplo:

• A projeção ortogonal mínima de um triângulo nas linhas situadas no plano do triângulo tem um comprimento igual à menor de suas altitudes.
• O corte reto mínimo em um plano através do qual uma placa triangular rígida pode ser tracionada deve ter comprimento igual à menor das alturas desta placa.
• Com o movimento contínuo de dois pontos ao longo do perímetro do triângulo em direção um ao outro, a distância máxima entre eles durante o movimento do primeiro encontro para o segundo não pode ser menor que o comprimento da menor altura do triângulo.
• A altura mínima em um triângulo sempre está dentro desse triângulo.

Relacionamentos básicos

• h a = b ⋅ sin ⁡ γ = c ⋅ sin ⁡ β , (\displaystyle h_(a)=b(\cdot )\sin \gamma =c(\cdot )\sin \beta ,)
• h a = 2 ⋅ S a , (\displaystyle h_(a)=(\frac (2(\cdot )S)(a)),) Onde S (\estilo de exibição S)- área de um triângulo, uma (\estilo de exibição a)- o comprimento do lado do triângulo pelo qual a altura é reduzida.
• h a = b ⋅ c 2 ⋅ R , (\displaystyle h_(a)=(\frac (b(\cdot )c)(2(\cdot )R)),) Onde b ⋅ c (\estilo de exibição b(\cdot )c)- produto dos lados, R − (\estilo de exibição R-) raio do círculo circunscrito
• h a: h b: h c = 1 a: 1 b: 1 c = (b ⋅ c) : (a ⋅ c) : (a ⋅ b) . (\displaystyle h_(a):h_(b):h_(c)=(\frac (1)(a)):(\frac (1)(b)):(\frac (1)(c)) =(b(\cdot )c):(a(\cdot )c):(a(\cdot )b).)
• 1 h a + 1 h b + 1 h c = 1 r (\displaystyle (\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_ (c)))=(\frac(1)(r))), Onde r (\estilo de exibição r)- raio do círculo inscrito.
• S = 1 (1 ha + 1 h b + 1 h c) ⋅ (1 ha + 1 h b - 1 h c) ⋅ (1 ha + 1 h c - 1 h b) ⋅ (1 h b + 1 h c - 1 h a) (\ displaystyle S =(\frac (1)(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b)))+(\frac (1)(h_(c ))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\frac (1)(h_(c))) )(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1)(h_(b))))(\ cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_(a))))))))), Onde S (\estilo de exibição S)- área de um triângulo.
• a = 2 ha ⋅ (1 ha + 1 h b + 1 h c) ⋅ (1 ha + 1 h b - 1 h c) ⋅ (1 ha + 1 h c - 1 h b) ⋅ (1 h b + 1 h c - 1 h a) (\ estilo de exibição a=(\frac (2)(h_(a)(\cdot )(\sqrt (((\frac (1)(h_(a)))+(\frac (1)(h_(b))) +(\frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(b)))-(\ frac (1)(h_(c))))(\cdot )((\frac (1)(h_(a)))+(\frac (1)(h_(c)))-(\frac (1 )(h_(b))))(\cdot )((\frac (1)(h_(b)))+(\frac (1)(h_(c)))-(\frac (1)(h_ (a))))))))), uma (\estilo de exibição a)- o lado do triângulo para o qual a altura desce ha (\estilo de exibição h_(a)).
• Altura de um triângulo isósceles baixado até a base: h c = 1 2 ⋅ 4 a 2 − c 2 , (\displaystyle h_(c)=(\frac (1)(2))(\cdot )(\sqrt (4a^(2)-c^(2)) ),)

Onde c (\estilo de exibição c)- base, uma (\estilo de exibição a)- lado.

Teorema da Altitude do Triângulo Retângulo

Se a altitude em um triângulo retângulo ABC tem comprimento h (\estilo de exibição h) desenhado a partir do vértice de um ângulo reto, divide a hipotenusa pelo comprimento c (\estilo de exibição c) em segmentos m (\estilo de exibição m) E n (\estilo de exibição n), correspondente às pernas b (\estilo de exibição b) E uma (\estilo de exibição a), então as seguintes igualdades são verdadeiras.

Ao resolver problemas geométricos, é útil seguir esse algoritmo. Ao ler as condições do problema, é necessário

• Faça um desenho. O desenho deve corresponder tanto quanto possível às condições do problema, portanto sua principal tarefa é ajudar a encontrar a solução
• Coloque todos os dados da definição do problema no desenho
• Anote todos os conceitos geométricos que aparecem no problema
• Lembre-se de todos os teoremas relacionados a esses conceitos
• Desenhe no desenho todas as relações entre os elementos de uma figura geométrica que decorrem desses teoremas

Por exemplo, se o problema contiver as palavras bissetriz de um ângulo de um triângulo, você precisará lembrar a definição e as propriedades de uma bissetriz e indicar segmentos e ângulos iguais ou proporcionais no desenho.

Neste artigo você encontrará as propriedades básicas de um triângulo que você precisa saber para resolver problemas com sucesso.

TRIÂNGULO.

Área de um triângulo.

1. ,

aqui - um lado arbitrário do triângulo - a altura baixada para este lado.

2. ,

aqui e são lados arbitrários do triângulo, e é o ângulo entre esses lados:

3. Fórmula de Heron:

Aqui estão os comprimentos dos lados do triângulo, é o semiperímetro do triângulo,

4. ,

aqui está o semiperímetro do triângulo e é o raio do círculo inscrito.

Sejam os comprimentos dos segmentos tangentes.

Então a fórmula de Heron pode ser escrita da seguinte forma:

5.

6. ,

aqui - os comprimentos dos lados do triângulo, - o raio do círculo circunscrito.

Se um ponto for tomado no lado de um triângulo que divide este lado na proporção m: n, então o segmento que conecta este ponto ao vértice do ângulo oposto divide o triângulo em dois triângulos, cujas áreas estão na proporção m: n:

A proporção das áreas de triângulos semelhantes é igual ao quadrado do coeficiente de similaridade.

Mediana de um triângulo

Este é um segmento que conecta o vértice de um triângulo ao meio do lado oposto.

Medianas de um triângulo se cruzam em um ponto e são divididos pelo ponto de interseção na proporção de 2:1, contando a partir do vértice.

O ponto de intersecção das medianas de um triângulo regular divide a mediana em dois segmentos, o menor dos quais é igual ao raio do círculo inscrito e o maior é igual ao raio do círculo circunscrito.

O raio do círculo circunscrito é duas vezes o raio do círculo inscrito: R=2r

Comprimento médio triângulo arbitrário

,

aqui - a mediana desenhada ao lado - os comprimentos dos lados do triângulo.

Bissetriz de um triângulo

Este é o segmento bissetriz de qualquer ângulo de um triângulo conectando o vértice desse ângulo com o lado oposto.

Bissetriz de um triângulo divide um lado em segmentos proporcionais aos lados adjacentes:

Bissetrizes de um triângulo se cruzam em um ponto, que é o centro do círculo inscrito.

Todos os pontos da bissetriz do ângulo são equidistantes dos lados do ângulo.

Altura do triângulo

Este é um segmento perpendicular que cai do vértice do triângulo para o lado oposto, ou sua continuação. Em um triângulo obtuso, a altitude traçada a partir do vértice do ângulo agudo fica fora do triângulo.

As alturas de um triângulo se cruzam em um ponto, que é chamado ortocentro do triângulo.

Para encontrar a altura de um triângulo desenhado ao lado, você precisa encontrar sua área de qualquer forma disponível e, em seguida, usar a fórmula:

Centro da circunferência circunscrita a um triângulo, encontra-se no ponto de intersecção das bissetoras perpendiculares traçadas aos lados do triângulo.

Raio da circunferência de um triângulo pode ser encontrado usando as seguintes fórmulas:

Aqui estão os comprimentos dos lados do triângulo e é a área do triângulo.

,

onde é o comprimento do lado do triângulo e é o ângulo oposto. (Esta fórmula segue do teorema do seno.)

Desigualdade triangular

Cada lado do triângulo é menor que a soma e maior que a diferença dos outros dois.

A soma dos comprimentos de quaisquer dois lados é sempre maior que o comprimento do terceiro lado:

Oposto ao lado maior está o ângulo maior; Oposto ao ângulo maior está o lado maior:

Se , então vice-versa.

Teorema dos senos:

Os lados de um triângulo são proporcionais aos senos dos ângulos opostos:

Teorema do cosseno:

O quadrado de um lado de um triângulo é igual à soma dos quadrados dos outros dois lados sem o dobro do produto desses lados pelo cosseno do ângulo entre eles:

Triângulo retângulo

- Este é um triângulo cujo ângulo é de 90°.

A soma dos ângulos agudos de um triângulo retângulo é 90°.

A hipotenusa é o lado oposto ao ângulo de 90°. A hipotenusa é o lado mais longo.

Teorema de Pitágoras:

o quadrado da hipotenusa é igual à soma dos quadrados dos catetos:

O raio de um círculo inscrito em um triângulo retângulo é igual a

,

aqui está o raio do círculo inscrito, - as pernas, - a hipotenusa:

Centro da circunferência circunscrita a um triângulo retângulo fica no meio da hipotenusa:

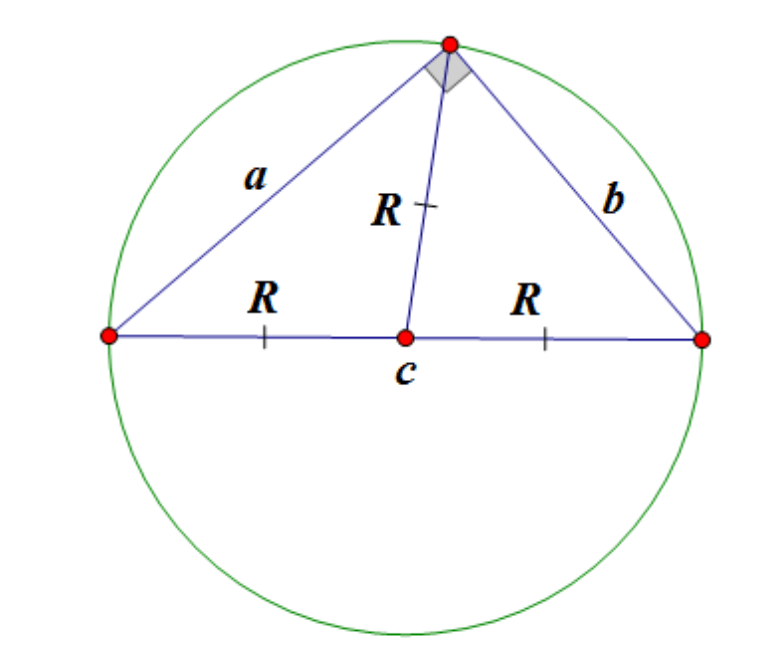
Mediana de um triângulo retângulo desenhado em direção à hipotenusa, é igual à metade da hipotenusa.

Definição de seno, cosseno, tangente e cotangente de um triângulo retângulo olhar

A proporção dos elementos em um triângulo retângulo:

O quadrado da altura de um triângulo retângulo desenhado a partir do vértice de um ângulo reto é igual ao produto das projeções dos catetos na hipotenusa:

O quadrado do cateto é igual ao produto da hipotenusa pela projeção do cateto na hipotenusa:

Perna deitada em frente ao canto igual à metade da hipotenusa:

Triângulo isósceles.

A bissetriz de um triângulo isósceles desenhada até a base é a mediana e a altitude.

Em um triângulo isósceles, os ângulos da base são iguais.

Ângulo do ápice.

E - lados,

E - ângulos na base.

Altura, bissetriz e mediana.

Atenção! A altura, bissetriz e mediana desenhadas ao lado não coincidem.

Triângulo regular

(ou Triângulo Equilátero ) é um triângulo cujos lados e ângulos são iguais entre si.

Área de um triângulo regular igual a

onde é o comprimento do lado do triângulo.

Centro de uma circunferência inscrita num triângulo regular, coincide com o centro do círculo circunscrito a um triângulo regular e fica no ponto de intersecção das medianas.

Ponto de intersecção das medianas de um triângulo regular divide a mediana em dois segmentos, o menor dos quais é igual ao raio do círculo inscrito e o maior dos quais é igual ao raio do círculo circunscrito.

Se um dos ângulos de um triângulo isósceles for 60°, então o triângulo é regular.

Linha média do triângulo

Este é um segmento que conecta os pontos médios de dois lados.

Na figura DE é a linha média do triângulo ABC.

A linha média do triângulo é paralela ao terceiro lado e igual à sua metade: DE||AC, AC=2DE

Ângulo externo de um triângulo

Este é o ângulo adjacente a qualquer ângulo do triângulo.

Um ângulo externo de um triângulo é igual à soma de dois ângulos não adjacentes a ele.

Funções trigonométricas do ângulo externo:

Sinais de igualdade de triângulos:

1 . Se dois lados e o ângulo entre eles de um triângulo são respectivamente iguais a dois lados e o ângulo entre eles de outro triângulo, então esses triângulos são congruentes.

2 . Se um lado e dois ângulos adjacentes de um triângulo são respectivamente iguais a um lado e dois ângulos adjacentes de outro triângulo, então esses triângulos são congruentes.

3 Se três lados de um triângulo são respectivamente iguais a três lados de outro triângulo, então esses triângulos são congruentes.

Importante: como em um triângulo retângulo dois ângulos são obviamente iguais, então para igualdade de dois triângulos retângulosé necessária igualdade de apenas dois elementos: dois lados, ou um lado e um ângulo agudo.

Sinais de semelhança de triângulos:

1 . Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e os ângulos entre esses lados são iguais, então esses triângulos são semelhantes.

2 . Se três lados de um triângulo são proporcionais a três lados de outro triângulo, então os triângulos são semelhantes.

3 . Se dois ângulos de um triângulo são iguais a dois ângulos de outro triângulo, então os triângulos são semelhantes.

Importante: Em triângulos semelhantes, os lados semelhantes estão opostos a ângulos iguais.

Teorema de Menelau

Deixe uma linha cruzar um triângulo, e é o ponto de sua intersecção com o lado, é o ponto de sua intersecção com o lado, e é o ponto de sua intersecção com a continuação do lado. Então